Uno studente scrive:
Oggetto: Pitagora ed euclide
Corpo del messaggio:
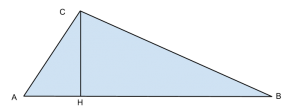
Determinare il perimetro di un triangolo rettangolo, sapendo che l’area è 600 cm^2 e che l’ipotenusa è uguale ai 25/9 della proiezione di un cateto su di essa. [risultato 2P=120]
Risposta dello staff
Dai dati abbiamo che:
![]()
![]()
Da qui avremo che:
![]()
Quindi possiamo anche calcolare che:
![]()
Per il secondo teorema di Euclide avremo che:
![]()
![]()
Mettendo tutto sotto radice quadrata otteniamo facilmente:
![]() .
.
Sfruttando ora la conoscenza dell’area troviamo l’ipotenusa:
![]()
![]()
![]()
![]()
Da qui avremo:
![]()
![]()
![]()
Troviamo i due cateti con il primo teorema di Euclide:
![]()
![]()
Quindi potremo calcolare il perimetro:
![]()
(Questa pagina è stata visualizzata da 367 persone)
Perfetto e velocissimo, grazie mille per la disponibilità 😀