Uno studente scrive:

 

Corpo del messaggio:
1)In un triangolo rettangolo, il cui perimetro è 30m, la proiezione di un cateto sull’ ipotenusa è 144/25 della proiezione dell’ altro cateto. Determina la lunghezza dell’ ipotenusa.

2) L’ area di un trapezio isoscele è . Sapendo che tale trapezio è circoscritto ad una circonferenza di raggio , determina la misura dei suoi lati.

 

 

 

 

Risposta dello staff

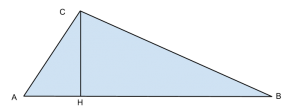
1)In un triangolo rettangolo, il cui perimetro è 30m, la proiezione di un cateto sull’ ipotenusa è 144/25 della proiezione dell’ altro cateto. Determina la lunghezza dell’ ipotenusa.

 

Dai dati sappiamo che:

Ponendo , troviamo tutto in funzione dell’incognita:

Sfruttiamo il primo teorema di Euclide per trovare i due cateti:

Quindi sfruttando la conoscenza del perimetro, otteniamo:

Quindi l’ipotenusa sarà:

 

 

 

2) L’ area di un trapezio isoscele è . Sapendo che tale trapezio è circoscritto ad una circonferenza di raggio , determina la misura dei suoi lati.

 

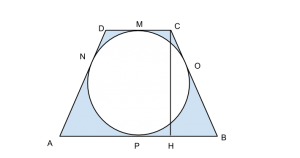
Tra le proprietà di un quadrilatero circoscritto utilizziamo quella per cui i segmenti di congruenza risultano essere uguali e quella che implica l’uguaglianza della somma dei lati opposti.

 

Da qui avremo, indicando con

e con

.

Quindi avremo che, notando che l’altezza equivale al diametro:

Quindi:

Notiamo anche che:

Sfruttiamo quindi il teorema di pitagora sul triangolo

Da qui avremo due numeri di cui sappiamo somma e prodotto, e quindi potremo risolvere l’equazione di secondo grado:

.

Da cui:

 

(Questa pagina è stata visualizzata da 476 persone)