Anna scrive: Esercizio principio di induzione

Oggetto: soluzione di un esercizioCorpo del messaggio:

ciao ti chiedo di risolvere questo esercizio: dimostrare tramite il principio di induzione 2.4.6. ….2n=2^n n fattoriale

$2=2^1 \cdot 1! =2$
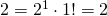
Supponiamo vero che 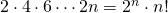$2\cdot 4 \cdot 6 \cdots 2n = 2^n \cdot n!$ , allora si dovrebbe verificare che 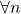$\forall n$ sia:

$2\cdot 4 \cdots 2n \cdot 2(n+1) =2^{n+1}(n+1)!$

Per semplificare chiamiamo con

$A=2\cdot 4 \cdot 6 \cdots 2n$

e con

$B=2^n \cdot n!$ .

Sappiamo che $A=B$ , e quindi:

$A \cdot 2(n+1) =2 \cdot 2^{n}[(n+1) n!]$

$A \cdot 2(n+1) =2 (n+1)\cdot 2^{n} n!$

$A \cdot 2(n+1) =2 (n+1) \cdotB$ .

$2(n+1) =2 (n+1)$ .

Questa identità è, ovviamente, sempre verificata.

cvd…

(Questa pagina è stata visualizzata da 132 persone)

Matebook