Giulia scrive: Soluzione esercizi fatti tutti tranne il 2 che non capisco…

Pubblicato il da Lo Staff2 commenti
0

Oggetto: Soluzioni esercizi

Corpo del messaggio:
Salve, avevo già scritto e mi è stato molto utile il vostro aiuto. Di seguito pubblico ulteriori esercizi da svolgere, poiché non sono riuscita a pubblicarli nella richiesta precedente. Se fosse possibile, desidererei i risultati esatti 🙂 grazie ancora! 🙂

image(1)

 

Risposta dello staff

1)

cos \alpha=-\frac 45

Calcoliamo il seno:

sen \alpha=- \sqrt{1-cos^2 \alpha}=-\sqrt{1-\frac {16}{25}}=-\sqrt{\frac{9}{25}}=-\frac 35

La tangente sarà:

tg \alpha=\frac {-\frac 35}{-\frac 45}=\frac 34.

2)

Non riesco a leggere la traccia……

3)

sen(\alpha+\beta)=sen\alpha cos \beta + sen \beta cos\alpha

Quindi:

sen(\frac 14 \pi+\frac 16 \pi)=sen\frac 14 \pi cos \frac 16 \pi + sen \frac 16 \pi cos\frac 14 \pi=\frac {\sqrt 6}{4}+\frac {\sqrt 2}{4}

4)

Basterà studiare la negatività del \Delta:

\Delta=(2k-1)^2-4k^2

4k^2-4k+1-4k^2<0

k>\frac 14.

5)

2-cos^2x >0 è sempre verificata senza bisogno di far calcoli perchè il coseno è una funzione compresa tra -1 e 1, e lo stesso vale per il quadrato. Quindi il minimo valore che potrà assumere è 1!!!

6)

2^x\left(2^x+1\right))=0

non sarà mai verificata perchè 2^x>0 per ogni x e di conseguenza anche l’altro fattore 2^x+1 sarà strettamente positivo.

7)

\begin{cases} log_{\frac 13} (x^2-9) >0 \\ x^2-9 >0 \end{cases}

\begin{cases} x^2-9<\left(\frac 13 \right)^0 \\ x^2-9 >0 \end{cases}

\begin{cases} x^2-9<1 \\ x<-3 \quad \lor \quad x >3 \end{cases}

\begin{cases} x^2<10 \\ x<-3 \quad \lor \quad x >3 \end{cases}

\begin{cases} -\sqrt{10}<x<\sqrt{10} \\ x<-3 \quad \lor \quad x >3 \end{cases}

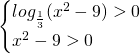
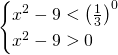
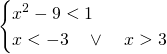
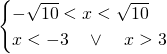
La soluzione sarà:

-\sqrt{10}<x<-3 \quad \lor \quad 3 <x<\sqrt{10}

8)

\frac{2^{-1}+\frac 14}{3^{-2}\cdot 27^{\frac 13}}=\frac {\frac 12 + \frac 14}{\frac 19 \cdot 3}=

=\frac {\frac 34}{\frac 13}=\frac 94

 

9)

cos 330^\circ=cos 30^\circ=sen 60^\circ

10)

\sqrt{x^2+4}<- \left|x\right|

Questa disequazione non ammetterà mai soluzione in quanto:

x^2+4 risulta essere sempre un numero positivo e lo stesso dicasi per la sua radice.

-\left|x\right| sarà sempre un numero negativo, a prescindere dal valore della x.

11)

log_2(x+1) \leq 1

\begin{cases} x+1 \leq 2^1 \\ x+1 >0 \end{cases}

\begin{cases} x \leq 1 \\ x >-1 \end{cases}

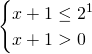
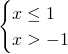
La soluzione è : -1<x\leq 1.

(Questa pagina è stata visualizzata da 160 persone)

2 pensieri riguardo “Giulia scrive: Soluzione esercizi fatti tutti tranne il 2 che non capisco…”

  1. Grazie mille! 🙂 avevo anche riscritto gli esercizi per email, in modo da poter essere più chiari 🙂 non fa nulla per il num 2, grazie mille davvero!! :):)

Lascia un commento