Oggetto: problema triangolo rettangolo

Corpo del messaggio:
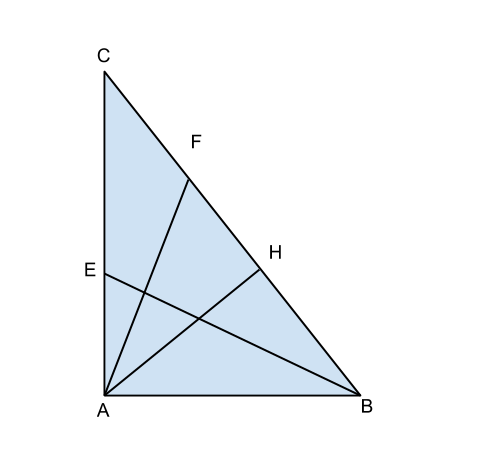
In un triangolo rettangolo ABC, l’ipotenusa BC è lunga e il cateto AB è 3/4 AC. Calcola la lunghezza della bisettrice BE dell’angolo B. Disegna l’altezza AH relativa all’ipotenusa e traccia la bisettrice AF dell’angolo CAH. Dimostra che le due bisettrici BE e AF sono perpendicolari e calcola la distanza del vertice A dalla bisettrice BE.
Grazie.

Risposta dello staff

Calcoliamo subito i cateti sapendo che:

e utilizzando Pitagora avremo:

Sapendo che BE è bisettrice, avremo che:

Ponendo avremo:

Ma sappiamo anche che:

Col teorema di Pitagora ricaviamo BE:

Consideriamo adesso i triangoli ACB e ABH. Ovviamente questi due triangoli saranno simili.

Da questo ricaviamo che:

Quindi le bisettrici formeranno angoli uguali, ovvero:

Da questa, chiamando O il punto di intersezione tra AF e BE, noteremo che, il triangolo AOE e BAE sono simili in quanto:

e hanno l’angolo  in comune e quindi il triangolo AOE è rettangolo.

Quindi, calcolare la distanza del vertice dalla bisettrice equivale a calcolare la lunghezza del segmento AO, che ricaviamo dalla similitudine:

 

(Questa pagina è stata visualizzata da 142 persone)