Esercizio 1 Funzione razionale fratta

$y=\frac{2x-1}{x-3}$

Insieme di definizione

Essendo una funzione razionale fratta, bisognerà escludere quei valori che annullano il denominatore, e quindi il dominio è tutto $\mathbb{R}-\{3\}$ , o scritto sotto forma di intervalli:

$D=]-\infty; 3 [ \quad \cup \quad ]3;+\infty [$

Simmetrie e periodicità

$-f(x)=\frac{-2x+1}{x-3}$

$f(-x)=\frac{-2x-1}{-x-3}$

Questa funzione non avrà simmetrie.

Intersezioni con gli assi

$\begin{cases} x=0 \\ y=\frac 13 \end{cases}$

$\begin{cases} y=0 \\ x=\frac 12 \end{cases}$

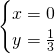
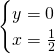
La funzione avrà due intersezioni con gli assi:

$\left (0;\frac 13 \right)$ e $\left (\frac 12;0 \right)$

Segno della funzione

Studiamo la positività di $f(x)$ :

$\frac{2x-1}{x-3} \geq0$

Studiamo separatamente numeratore e denominatore:

$2x-1 \geq 0 \rightarrow x \geq 12$

$x-3 >0 \rightarrow x > 3$

$x \leq \frac 12 \quad \lor \quad x >3$

condizione agli estremi

$\lim_{ x \rightarrow \pm \infty} f(x)= 2$

$\lim_{ x \rightarrow 3^-} f(x)= -\infty$

$\lim_{ x \rightarrow 3^+} f(x)= +\infty$

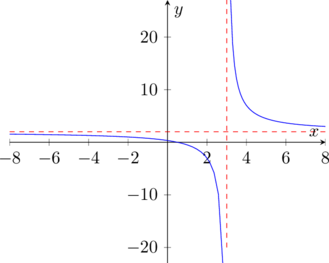
Asintoti

La funzione avrà asintoto verticale in $x=3$ e asintoto orizzontale in $y=2$

Studio della derivata prima

$y'=\frac{2(x-3)-(2x-1)}{(x-3)^2}=\frac{-5}{(x-3)^2}$

$y' \geq 0$

$\frac{-5}{(x-3)^2} \geq0$

Visto che questa disequazione non sarà mai verificata, la funzione sarà sempre decrescente per ognuno dei suoi due intervalli, quindi è decrescente in $x<3$ e sarà decrescente per $x>3$ . Non avrà massimi e minimi relativi

Studio della derivata seconda

$y''=\frac {10}{(x-3)^3}$

$y''\geq 0$

$\frac {10}{(x-3)^3} \geq0$

$x>3$

La funzione avrà concavità verso il basso fino nell’intervallo $]-\infty; 3 [$ e concavità verso l’alto nell’intervallo $]3;+\infty [$

Rendered by QuickLaTeX.com

Altri esercizi simili:

(Questa pagina è stata visualizzata da 52 persone)

Lascia un commento Annulla risposta