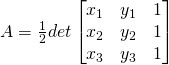Triangoli qualsiasi

0

Triangoli qulasiasi

Legenda

 
AB=c, \, AC=b, \, BC=a AH=h, \mbox{ altezza}
\widehat{BAC}=\alpha, \, \widehat{ABC}=\beta, \, \widehat{ACB}= \gamma AM=m, \mbox{ mediana}
AD=d, \mbox{ bisettrice angolo esterno} AI=l, \mbox{ bisettrice}
p=\frac 12(a+b+c), \mbox{ semiperimetro} A=\mbox{ area}
Proprietà

\left| b-c \right | < a < b+c; \, \, \left| a-c \right | < b < a+c;

\, \, \left| a-b \right | < c < a+b
a>b \Leftrightarrow \alpha > \Beta
\alpha+\beta+\gamma=\pi

 
Calcolo dell’area
A=\frac {b\cdot h}{2} a=\frac {a\cdot c\cdot sen\gamma}{2}=\frac {a\cdot c\cdot sen\beta}{2}=\frac {b \cdot c\cdot sen\alpha}{2}

A=\sqrt {p\cdot(p-a)\cdot(p-b)\cdot(p-c)}

(Formula di Erone)

 A=\frac 1 2 \cdot a^2 \cdot \frac {sen \beta \cdot sen \gamma}{sen \alpha}
A=p^2\cdot tg \frac {\alpha}{2}\cdot tg \frac {\beta}{2}\cdot tg \frac {\gamma}{2}

Sul piano cartesiano, sapendo le coordinate dei vertici:

A=\frac 12 det \begin{bmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{bmatrix}

m_a=\frac 12 \cdot \sqrt {2b^2+2c^2-a^2};

m_b=\frac 12 \cdot \sqrt {2a^2+2c^2-b^2};

m_c=\frac 12 \cdot \sqrt {2a^2+2b^2-c^2}

  Lunghezza delle mediane
AB^2+BC^2=2(BM^2+AM^2) Teorema della mediana
BI:IC=AB:AC Teorema della bisettrice dell’angolo interno
CD:BD=AC:AB(se i segmenti esistono) Teorema della bisettrice dell’angolo esterno

R=\frac {abc}{4A}

R=\frac {a}{2sen\alpha}; \,R=\frac {b}{2sen\beta}; \, R=\frac {c}{2sen\gamma}

 Raggio della circonferenza circoscritta 

r=\frac Ap; \, r= \sqrt {\frac {(p-a)(p-b)(p-c)}{p}}

r=(p-a)\cdot tg \frac {\alpha}{2};

r=(p-b)\cdot tg \frac {\beta}{2};

r=(p-c)\cdot tg \frac {\gamma}{2}

 Raggio della circonferenza inscritta 

r_a= \sqrt {\frac {p(p-b)(p-c)}{p-a}};

r_b= \sqrt {\frac {p(p-a)(p-c)}{p-b}};

r_c= \sqrt {\frac {p(p-a)(p-b)}{p-c}}

r_a= p\cdot tg \frac {\alpha}{2};

r_b=p \cdot tg \frac {\beta}{2};

r_c= p \cdot tg \frac {\gamma}{2}

 Raggio della circonferenza exinscritta 
Altezze
Teorema dei seni: In un triangolo è costante il rapporto tra la misura di un lato e il seno dell’angolo opposto
Teorema della corda: In un triangolo il rapporto tra la misura di un lato e il seno dell’angolo opposto è uguale al diametro della circonferenza circoscritta

 

 

 

Altri hanno visualizzato anche:

(Questa pagina è stata visualizzata da 179 persone)

Lascia un commento