Dilatazioni

Si definisce dilatazione $\delta(m;n)$ di centro $O(0;0)$ e rapporti $m$ e $n$ , con $m,n \in R^*$ , la trasformazione piana che ad ogni punto $P(x;y)$ del piano fa corrispondere il punto $P'(x';y')$ in modo che valgano le equazioni

$\delta(m;n) = \bigg \{ \begin{array}{rl} x'=mx \\ y'=ny \\ \end{array}$

Dilatazione dirette $\Leftrightarrow m \cdot n >0$ ;
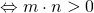il centro 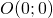$O(0;0)$ è l’unico punto unito;
gli assi cartesiani sono rette unite.

Si definisce dilatazione $\delta(m;n)$ di centro $C(x_C;y_C)$ e rapporti $m$ e $n$ , con $m,n \in R^*$ , la trasformazione piana che ad ogni punto $P(x;y)$ del piano fa corrispondere il punto $P'(x';y')$ in modo che valgano le equazioni

$\delta(m;n) = \bigg \{ \begin{array}{rl} x'-x_C=m(x-x_C) \\ y'-y_C=n(y-y_C) \\ \end{array}$ ,

ovvero

$\delta(m;n) = \bigg \{ \begin{array}{rl} x'=mx+p \\ y=ny+q \\ \end{array}$ ,

Dilatazione dirette $\Leftrightarrow m \cdot n >0$ ;
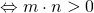il centro 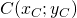$C(x_C;y_C)$ è l’unico punto unito;
le rette parallele agli assi cartesiani e passanti per il centro 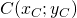$C(x_C;y_C)$ sono rette unite.

Se a una circonferenza di raggio $r$ si applica una dilatazione $\delta (m;m)$ di rapporti $m$ e $n$ si ottiene un’ellisse caratterizzata dai parametri $a=mr$ e $b=nr$ .

Se i rapporti $m$ e $n$ sono uguali, la dilatazione $\delta (m;n)$ coincide con l’omotetia di ugual centro e di rapporto $m$ .

Altri hanno visualizzato anche:

(Questa pagina è stata visualizzata da 735 persone)

Matebook

La matematica spiegata passo passo

Un pensiero riguardo “Dilatazioni”

Lascia un commento Annulla risposta