Problema 2.2 Scientifico 2011

Sia $f$ la funzione definita sull’insieme R dei numeri reali da

$f (x) = (ax + b) e^{-\frac x3} + 3.$

dove a e b sono due reali che si chiede di determinare sapendo che $f$ ammette un massimo nel punto d’ascissa 4 e che $f(0) = 2$ .

Si studi su R la funzione $f (x) = (x - 1) e^{-\frac x3} + 3$ e se ne tracci il grafico $\Gamma$ nel sistema di riferimento $Oxy$ .

Studiamo quindi la funzione appena trovata.

Essendo una funzione razionale intera che moltiplica un’esponenziale, l’unico problema per il dominio riguarda l’esponente. Ma non essendoci l’incognita a denominatore, allora il dominio sarà l’insieme dei numeri reali, quindi:

$D=R$ .

Notiamo che: $f(-x)=(-x - 1) e^{\frac x3} + 3 \neq \pm f(x)$ , e quindi non presenta simmetrie.

Le intersezioni con l’asse delle ascisse non risulteranno di immediato calcolo, e quindi ci limiteremo solo a studiare l’intersezione con l’asse delle ordinate e in seguito approssimeremo le altre.

$\begin{cases} x=0 \\ y=f(x) \end{cases}$

$\begin{cases} x=0 \\ y=2 \end{cases}$

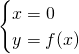
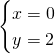
Studiamo i limiti negli estremi del dominio:

$\lim_{x \to -\infty} f(x)= -\infty.$

Non presenta asintoti obliqui a sinistra poichè:

$\lim_{x \to -\infty} \frac {f(x)}{x}= +\infty.$

Studiamo a $+\infty$ :

$\lim_{x \to +\infty} f(x)= \lim_{x \to +\infty} \frac {x-1}{e^{\frac x3}}+3 \mbox { forma indeterminata }.$

Applico de L’Hopital:

$\lim_{x \to +\infty} \frac {1}{\frac 13e^{\frac x3}}=0.$

Quindi avremo che:

$\lim_{x \to +\infty} f(x)=3$

e $y=3$ risulta essere asintoto orizzontale.

Studiamo la derivata prima, già calcolata nel primo punto:

$f'(x)=\frac 13e^{-\frac x3}\left(4-x \right).$

La funzione sarà derivabile in tutto R, e avremo che $f'$ è positiva (f crescente) per $x<4$ , negativa (f decrescente) per $x>4$ e ammetterà un punto di massimo in $x=4$ . (come già detto nella traccia..)