Quesito 9

0

f(x)=\begin{cases} x^3 \quad 0 \leq x \leq 1 \\ x^2-kx+k \quad 1<x\leq 2 \end{cases}

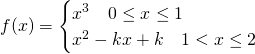
Affinchè possiamo applicare il Teorema di Lagrange in [0;2], la funzione deve essere continua nell’intervallo chiuso e derivabile nell’intervallo aperto.

Ora, visto che, nei singoli tratti la funzione è continua, vediamo nel punto x=1 se la funzione è continua:

f(1^-)=1^3=1

f(1^+)=1-k+k=1

Quindi, la funzione è continua in 1 per qualsiasi valore di k. Verifichiamo la derivabilità:

f'(x)=\begin{cases} 3x^2 \quad 0 \leq x \leq 1 \\ 2x-k \quad 1<x\leq 2 \end{cases}

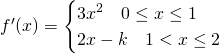
Anche qui, nei singoli tratti è derivabile. Verifichiamo per quale valore di k la funzione è derivabile in 1:

f'(1^-)=3

f'(1^+)=2-k

Affinchè sia derivabile deve verificarsi che:

3=2-k

k=-1

La funzione è quindi:

f(x)=\begin{cases} x^3 \quad 0 \leq x \leq 1 \\ x^2+x-1 \quad 1<x\leq 2 \end{cases}

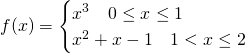
Ora bisogna trova un punto c \in (0;2) tale per cui:

f'(c)=\frac{f(b)-f(a)}{b-a}

f(b)=5

f(a)=0

Sostituendo avremo:

f'(c)=\frac 52

per cui, se fosse nel primo tratto sarebbe:

\frac 52=3c^2

c^2=\frac 56

c=\pm \sqrt{\frac 56}

Escludendo la possibilità che c sia negativo, visto il dominio, possiamo accettare la soluzione:

c= \sqrt{\frac 56}

in quanto compresa tra 0 e 1.

Verifichiamo che ce ne sia un secondo:

2c+1=\frac 52

2c=\frac 32

c=\frac 34

Ma, essendo \frac 34<1, non apparterrà al secondo tratto di funzione e quindi non è una soluzione accettabile.

(Questa pagina è stata visualizzata da 5 persone)

Lascia un commento