Daniela scrive: Derivate parziali

Pubblicato il da Lo Staff4 commenti
0

Oggetto:

Corpo del messaggio:

  • \frac {xy^2-2xy}{ x^2-y^2};
  • \frac {(x-y)^2}{(x-1)(y-1)}

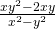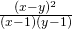
Derivate parziali prime rispetto a x e a y  e applicazione teorema Schwarz
(passaggio per passaggio).

Quando bisogna fare le derivate parziali bisogna considerare una alla volta le variabili come se fossero delle costanti, un numero…

\frac {\delta \, f}{\delta \, x}= \frac {(y^2-2y)(x^2-y^2)-(xy^2-2xy)(2x)}{(x^2-y^2)^2}=\frac {x^2y^2-y^4-2x^2y+2y^3-2x^2y^2+4x^2y}{(x^2-y^2)^2}=\frac {-y^4+2y^3-x^2y^2+2x^2y}{(x^2-y^2)^2}

\frac {\delta \, f}{\delta \, y}= \frac {(2xy-2x)(x^2-y^2)-(xy^2-2xy)(-2y)}{(x^2-y^2)^2}=\frac {2x^3y-2xy^3-2x^3+2xy^2+2xy^3-4xy^2}{(x^2-y^2)^2}=\frac {2x^3y-2x^3-2xy^2}{(x^2-y^2)^2}

\frac {\delta \, f}{\delta \, x}= \frac {2(x-y)(x-1)(y-1)-(x-y)^2(y-1)}{[(x-1)(y-1)]^2}=\frac {(x-y)(2x-2-x+y)}{(x-1)^2(y-1)}=\frac {(x-y)(x+y-2)}{(x-1)^2(y-1)}

\frac {\delta \, f}{\delta \, y}= \frac {-2(x-y)(x-1)(y-1)-(x-y)^2(x-1)}{[(x-1)(y-1)]^2}=\frac {(y-x)(2y-2-y+x)}{(x-1)(y-1)^2}=\frac {(y-x)(2y+x-2)}{(x-1)(y-1)^2}

 

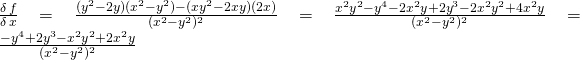
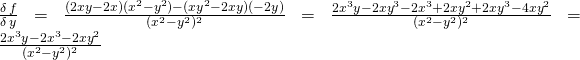
P.S. Prima di svolgere tutto, prova a fare le derivata di \frac {9x-6x}{ x^2-9},

ottenuta sostituendo 3 alla y, e di \frac {3y^2-6y}{ 9-y^2}, ottenuta sostituendo 3 alla x… Vedrai che otterrai esattamente lo stesso risultato di sopra, sostituendo i valori ottenuti alle incognite.

 

 

 

 

 

(Questa pagina è stata visualizzata da 235 persone)

4 pensieri riguardo “Daniela scrive: Derivate parziali”

  1. Per la prima funzione ero riuscita a risolverla, con i passaggi mi trovo con voi, vi ringrazio… 🙂
    Per la seconda
    2(x-y)(x-1)(y-1)- (x-y)^2(y-1)/(x-1)(y-1)^2
    potreste spiegarmi le semplificazioni adottate per giungere a questa forma:
    (x-y)(2x-2-x+y)/(x-1)^2(y-1)

  2. Innanzitutto al denominatore avrai (x-1)^2 (y-1)^2.

    A parte questo ho saltato il passaggio di messa in evidenza per i 2 fattori al numeratore di (x-y) e (y-1).
    così facendo, ho poi semplificato (y-1) al numeratore e al denominatore, ottenendo il risultato che leggi.

  3. si, ero riuscita a farlo, ero entrata nel sito per avvisarti:D

    Per la funzione
    z= √2x – 2 √y + √xy
    è giusto derivarla così:
    f'(x)= (1/2√2x )(2) + (1/2√xy)(y)
    f'(y)= (-2/2√y)(1) + (1/2 √xy)(x)

  4. si, ero riuscita a farlo, ero entrata nella pagina per avvisarti 🙂
    Per la funzione z= √2x-2√y+√xy
    è giusto derivarla così:
    f'(x)= (1/2 √2x)(2)+(1/2√xy)(y)
    f'(y)= (-2)(2 √y)(1) +(1/2 √xy)(x)

Lascia un commento