Kristina scrive: Funzioni goniometriche inverse

Pubblicato il 7 Gennaio 20167 Gennaio 2016 da Lo StaffLascia un commento

Oggetto: Funzioni goniometriche inverse

Corpo del messaggio:
a) Trova il dominio della funzione y=f(x)=arcsen|(2x-1)/x+radical arctg(2x-1)
b) Calcola f(1/2) e f(1)
c) Considera y=g(x)=a+barcosradical[(x-1)/x]
Per i quali valori dei parametri a e b il suo grafico interseca f(x) nel punto di ascissa 1 e taglia l’asse x nel punto di ascissa 2?
d) determina dominio di g(x)
Ps : non sono riuscita neanche a impostare questo problema, perche non si proprio come comportarmi con una funzione goniometrica inversa, in particolare mi potreste spiegare per favore disequazioni con questo tipo di funzioni? Grazie per l’aiuto

Risposta dello staff

Non capisco se all’inizio è un valore assoluto, ma la svolgiamo senza. Nel caso risolviamo anche nell’altro modo:

$y= arcsen \frac{2x-1}{x} + \sqrt{arctg(2x-1)}$

a)Studiamo il dominio (indifferente a prescindere che ci sia o meno il valore assoluto):

$\begin{cases} -1 \leq \frac{2x-1}{x} \leq 1 \\ arctg(2x-1) \geq 0 \end{cases}$

$\begin{cases} \frac{2x-1}{x} \geq -1 \\ \frac{2x-1}{x} \leq 1 \\ 2x-1 \geq 0 \end{cases}$

$\begin{cases} \frac{2x-1}{x}+1 \geq 0 \\ \frac{2x-1}{x}-1 \leq 0 \\ x \geq \frac 12 \end{cases}$

$\begin{cases} \frac{3x-1}{x} \geq 0 \\ \frac{x-1}{x} \leq 0 \\ x \geq \frac 12 \end{cases}$

$\begin{cases} x < 0 \quad \lor \quad x \geq \frac 13 \\ 0 < x \leq 1 \\ x \geq \frac 12 \end{cases}$

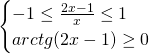
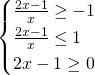
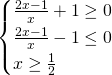
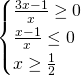
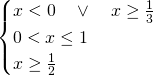
Il dominio sarà quindi:

$\frac 12 \leq x \leq 1$

b)

$f(\frac 12)=arcsen (0) + \sqrt{arctg(0)}=0$

$f(1)=arcsen (1) + \sqrt{arctg(1)}=\frac {\pi}{2}+ \frac {\pi}{4}=\frac 34 \pi$

c) Siano

$P(1;\frac 34 \pi)$ e $Q(2;0)$ ,

avremo:

$g(x)=a+b arcos \sqrt{\frac{x-1}{x}}$

da cui:

$\begin{cases} a+b \frac 12 \pi =\frac 34 \pi \\ a+b \frac 13 \pi = 0\end{cases}$

$\begin{cases} a+b \frac 12 \pi =\frac 34 \pi \\ a=-b \frac 13 \pi \end{cases}$

$\begin{cases} -b\frac 13 \pi +b \frac 12 \pi =\frac 34 \pi \\ a=-b \frac 13 \pi \end{cases}$

$\begin{cases} -4b +6b =9 \\ a=-b \frac 13 \pi \end{cases}$

$\begin{cases} b =\frac 92 \\ a=- \frac 32 \pi \end{cases}$

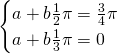
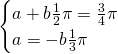
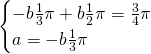
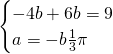
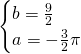
d)

il dominio di $g(x)$ è dato dal dominio dell’arccosen, ovvero basterà porre:

$-1 \leq \frac {x-1}{x} \leq 1$

da cui:

$\begin{cases} \frac{x-1}{x} \geq -1 \\ \frac{x-1}{x} \leq 1 \end{cases}$

$\begin{cases} \frac{x-1}{x}+1 \geq 0 \\ \frac{x-1}{x}-1 \leq 0 \end{cases}$

$\begin{cases} \frac{2x-1}{x} \geq 0 \\ \frac{-1}{x} \leq 0 \end{cases}$

$\begin{cases} x < 0 \quad \lor \quad x \geq \frac 12 \\ x >0 \end{cases}$

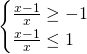
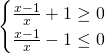
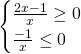
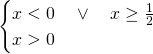
E il dominio sarà quindi:

$x \geq \frac 12$

(Questa pagina è stata visualizzata da 23 persone)

Lascia un commento Annulla risposta