Erika scrive: Esercizio principio di induzione

Pubblicato il da Lo StaffLascia un commento
0

Oggetto: SOLUZIONE

Corpo del messaggio:
ciao domani ho l’esame… potrest dirmi gentilmente come si risoove questo  principio di induzione’ 2^n maggiore n^2 con ( n maggiore e uguale 4)   e poi n^n  maggiore e uguale di n!  ti ringrazio e urgente!

Svolgimento

 

  • 2^n > n^2 \quad \mbox { con } \quad n \geq 4.

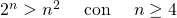Verifichiamo per 4:

2^4>4^2 \Rightarrow 16>16…

Quindi suppongo che nella traccia manchi qualcosa… (o un maggiore uguale nella formula iniziale oppure n non può essere maggiore uguale a 4…)

Cmq, andando avanti, ipotizzando che sia verificato per n, analizziamo il caso n+1…

2^{n+1}>(n+1)^2

2 \cdot 2^n>n^2+2n+1

Se abbiamo accettato l’ipotesi sapremo che:

2 \cdot 2^n > 2 \cdot n^2.

Verifichiamo quindi che:

2n^2 > n^2+2n+1

n^2>2n+1

n^2-2n-1>0.

Con un piccolo artificio possiamo afferamre che:

(n-1)^2-2>0

(n-1)^2>2;

e questa disequazione è verificata per qualsiasi n numero naturale maggiore a 3… CVD

 

  • n^n \geq n!

Supposto vero per n, verifichiamo per n+1:

(n+1)^{n+1} \geq (n+1)!

(n+1)(n+1)(n+1) \cdots (n+1) \geq (n+1) n!

Essendo di sicuro n+1 positivo, avremo che:

(n+1)^2 \geq n!

Di sicuro sappiamo che:

(n+1)^n > n^n

per qualsiasi n numero intero naturale e quindi, sapendo per ipotesi che:

n^n \geq n!, avremo che:

(n+1)^n \geq n!

 

CVD.

 

(Questa pagina è stata visualizzata da 159 persone)

Lascia un commento