Marco scrive: 4 esercizi – 1

n1 studio di funzione

$f(x)=3x+2logx$

Dominio:

$x > 0$

$D= \left(0;+\infty\right)$ .

Non ci saranno simmetrie, quindi la funzione non è ne pari ne dispari.

L’intersezione con l’asse delle ascisse non è immediata da calcolare, e la disegneremo qualitativamente.

Calcolando $f(1)=3$ , sapremo che uno zero della funzione sarà tra 0 e 1. Scopriremo dopo che questo sarà anche l’unico.

Calcoliamo i limiti negli estremi del dominio:

$\lim_{x \to +\infty} f(x)= +\infty$

$\lim_{x \to 0^+} f(x)= -\infty$

Non ci sono asintoti obliqui.

Calcoliamo la derivata prima:

$y'=3+\frac 2x$

Studiamo la positività della derivata prima, ma, ricordando che, nel dominio, avremo solo x positive la funzione sarà sempre crescente in esso.

Non ammetterà punti di massimo o di minimo.

Calcoliamo la derivata seconda:

$y''=-\frac{2}{x^2}$

Essendo la derivata seconda sempre negativa nel dominio, allora la funzione avrà sempre la concavità verso il basso.

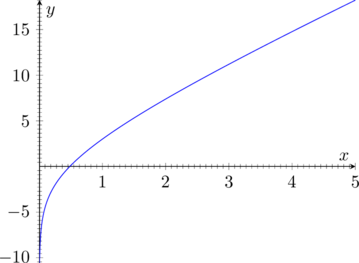
Ecco il grafico:

Rendered by QuickLaTeX.com

(Questa pagina è stata visualizzata da 72 persone)

Matebook