Nicolò scrive: Matematica

Oggetto: Matematica 1

Corpo del messaggio:
Aiutoooooo ho esame.

Risposta dello staff

Studiare l’andamento della funzione

$\begin{cases} f(x)=e^{-(x+1)^2} \, \, \, \mbox{ se } \, \, x \leq 0 \\ f(x)=x^2-x+\frac 1e \, \, \, \mbox{ se } \, \, x>0 \end{cases}$

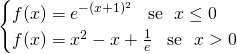
Descrivendone gli aspetti qualitativi e quantitativi. Disegnare un grafico.

Studiamo la funzione:

Il dominio è tutto R, in quanto nel primo tratto è una funzione esponenziale il cui esponente è un binomio, mentre la seconda è una funzione razionale intera.

La funzione è continua in 0 in quanto

$f(0^-)=e^{-1}=\frac 1e=f(0^+)$

Sarà sicuramente positiva per $x \leq0$ ; studiamo invece la positività nell’altro tratto:

$x^2-x+\frac 1e>0$

$\Delta=1-\frac 4e<0$

Essendo il $\Delta$ negativo allora l’equazione associata non ammetterà soluzioni, ovvero la funzione è sempre positiva anche nel secondo tratto.

Studiamo i limiti negli estremi:

$\lim_{x \to -\infty} f(x)=0$

$\lim_{x \to +\infty } f(x)=+\infty$

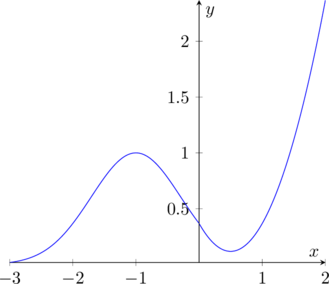
Notando che il secondo tratto è una parabola rivolta verso l’alto, il minimo sarà dato dal suo vertice. Verifichiamo che questo appartenga al suo dominio:

$V(-\frac {b}{2a};-\frac{\Delta}{4a})$