Oggetto: Matematica
Risposta dello staff
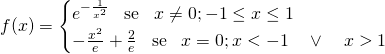
Dalla definizione della funzione ci accorgiamo che il dominio è tutto ![]()
Studiamo quindi la positività, notando che la funzione è sicuramente pari, essendoci solo termini quadratici:
![]()
Sicuramente sarà positiva per ![]() , essendo formata da una funzione esponenziale.
, essendo formata da una funzione esponenziale.
studiamo invece nel resto del dominio:
![]()
![]()
![]()
![]()
Unendo le due soluzioni, avremo:
![]()
![]()
![]()
Studiamo la continuità nei punti di contatto delle due funzioni:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
questi ultimi due erano superflui essendo simmetrica rispetto all’asse delle x ed avendolo già studiato per ![]()
Quindi avremo che la funzione in 0 nn è continua.
![]()
Studiamo la derivata prima:
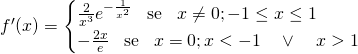
Da qui notiamo che:
![]()
![]()
![]()
![]()
![]()
(Questa pagina è stata visualizzata da 28 persone)
