Tre amici discutono animatamente di numeri reali. Anna afferma che sia i numeri razionali che gli irrazionali sono infiniti e dunque i razionali sono tanti quanti gli irrazionali. Paolo sostiene che gli irrazionali costituiscono dei casi eccezionali, ovvero che la maggior parte dei numeri reali sono razionali. Luisa afferma, invece, il contrario: sia i numeri razionali che gli irrazionali sono infiniti, ma esistono più numeri irrazionali che razionali. Chi ha ragione? Si motivi esaurientemente la risposta.

Di base sappiamo che:

.

.

Anche se da qui sembra immediato, vediamo come sia possibile “contare” i razionali, e come non sia possibile farlo per gli irrazionali…

Ipotizziamo di avere questa tabella

 

1        2        3

1        

2        

3        

Ordinando i numeri secondo le diagonali, posso contare i numeri di Q all’infinito.

 

Consideriamo ora gli irrazionali tra zero e 1, e supponiamo per assurdo di poterli ordinare tutti, scrivendoli così:

• 
• 
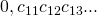
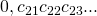
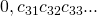• , e via dicendo…

dove le cifre .

Però, se consideriamo il numero irrazionale tra 0 e 1 che non ha come prima cifra decimale la cifra ,  come seconda cifra decimale la cifra e via discorrendo, ho trovato un numero che non avevo contato nell’elenco. Questo è un assurdo dovuto all’aver supposto di poterli contare tutti.

Di conseguenza Luisa ha ragione!!!

 

 

 

 

Altri esercizi simili

• Quesito 1 P.N.I. 2013
• Quesito 2 P.N.I. 2013
• Quesito 3 P.N.I. 2013
• Quesito 4 P.N.I. 2013
• Quesito 5 P.N.I. 2013
• Quesito 6 P.N.I. 2013
• Quesito 7 P.N.I. 2013
• Quesito 8 P.N.I. 2013
• Quesito 9 P.N.I. 2013
• Quesito 10 P.N.I. 2013

(Questa pagina è stata visualizzata da 23 persone)