In alcuni casi il calcolo dell’integrale indefinito risulta semplificato applicando il metodo di sostituzione in base al quale, assegnato l’integrale ![]() :
:
- si pone
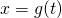 , con
, con 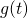 funzione di una variabile
funzione di una variabile 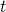 , derivabile e invertibile;
, derivabile e invertibile; - si determina il differenziale
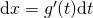 ;
; - si effettua la sostituzione nell’integrale assegnato ottenendo
![]() ;
;
- si calcola
![Rendered by QuickLaTeX.com \int f[g(t)] g'(t) \mathrm{d}t](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-c34ad11b6af92269efc1136822895123_l3.png) rispetto alla variabile
rispetto alla variabile 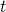 , ottenendo, per sostituzione, la soluzione dell’integrale
, ottenendo, per sostituzione, la soluzione dell’integrale 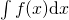 .
.
Si propongono alcune sostituzioni particolari:
Altri hanno visualizzato anche
[siblings depth=1]
(Questa pagina è stata visualizzata da 286 persone)