Geometria solida

0

Richiamo di teoria di geometria solida

 

Se una retta è perpendicolare a due altre, passanti per un medesimo punto, è perpendicolare a ogni retta del loro fascio, ma a nessuna altra retta della loro stella.

Se dal piede di una perpendicolare a un piano si conduce la perpendicolare a una retta di questo piano, il piano delle prime due rette è perpendicolare alla terza.

In un poliedro la somma fra il numero f delle facce e il numero v dei vertici è uguale al numero s degli spigoli aumentato di due.

Un prisma i cui spigoli laterali sono perpendicolari alle basi si dice retto.

Una piramide in cui la base è circoscrittibile a una circonferenza il cui centro è il piede dell’altezza si dice retta.

Le sezioni parallele alla base di un prisma sono tutte tra loro congruenti.

Le sezioni parallele alla base di una piramide sono poligoni simili; i loro perimetri sono proporzionali alle distanze delle sezioni dal vertice, le loro aree ai quadrati di tali distanze.

Un poliedro si dice regolare quando tutte le sue facce sono poligoni regolari congruenti tra loro e tutti gli angoloidi sono congruenti.

Principio di Cavalieri

Due solidi sono equivalenti se possono essere collocati rispetto a un piano in modo tale che ogni altro piano a esso parallelo determini su di essi sezioni equivalenti.

Volumi di figure solide

  • Prisma: 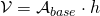\mathcal V = \mathcal A_{base} \cdot h, dove 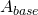A_{base} è l’area di base e 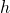h l’altezza.
  • Piramide: 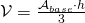\mathcal V = \frac {\mathcal A_{base} \cdot h}{3}, dove 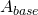A_{base} è l’area di base e 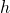h l’altezza.
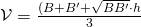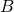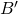  • Tronco di piramide: \mathcal V = \frac {(B+B'+\sqrt {BB'} \cdot h}{3}, dove B e B' sono le aree delle basu e 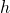h l’altezza.
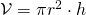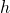  • Cilindro: \mathcal V = \pi r^2 \cdot h, dove r è il raggio di base e h l’altezza.
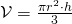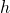  • Cono: \mathcal V = \frac {\pi r^2 \cdot h}{3}, dove r è il raggio di base e h l’altezza.
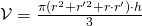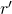  • Tronco di cono: \mathcal V = \frac {\pi (r^2+r'^2+r\cdot r') \cdot h}{3}, dove r e r' sono i raggi delle basi e 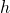h l’altezza.
  • Sfera: 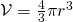\mathcal V=\frac 4 3 \pi r^3 dove r è il raggio.

 

 

(Questa pagina è stata visualizzata da 667 persone)

Lascia un commento