- Triangoli rettangoli
Considerato un triangolo rettangolo ![]() , si indicano con
, si indicano con ![]() il vertice dell’angolo retto, con
il vertice dell’angolo retto, con ![]() la lunghezza dell’ipotenusa, con
la lunghezza dell’ipotenusa, con ![]() e
e ![]() le lunghezze dei cateti opposti ai vertici
le lunghezze dei cateti opposti ai vertici ![]() e
e ![]() , con
, con ![]() le misure degli angoli di vertici rispettivamente
le misure degli angoli di vertici rispettivamente ![]() . Si ha pertanto
. Si ha pertanto ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
In un triangolo rettangolo si ha che:
- un cateto è uguale al prodotto dell’ipotenusa per il seno dell’angolo opposto al cateto considerato:
in formule ![]() e
e ![]() ;
;
- un cateto è uguale al prodotto dell’ipotenusa per il coseno dell’angolo adiacente al cateto considerato:
in formule ![]() e
e ![]() ;
;
- un cateto è uguale al prodotto dell’altro cateto per la tangente dell’angolo opposto al primo cateto considerato:
in formule ![]() e
e ![]() ;
;
- un cateto è uguale al prodotto dell’altro cateto per la cotangente dell’angolo adiacente al primo cateto considerato:
in formule ![]() e
e ![]() .
.
- Triangoli qualsiasi
Considerato un triangolo qualsiasi 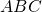 , si indicano con
, si indicano con 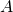 ,
, 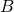 e
e 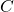 i vertici del triangolo, con
i vertici del triangolo, con  ,
, 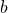 e
e  le lunghezze dei lati opposti rispettivamente ai tre vertici
le lunghezze dei lati opposti rispettivamente ai tre vertici 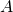 ,
, 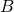 , e
, e 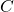 , con
, con 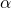 ,
, 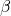 ,
, 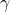 le misure degli angoli di vertici
le misure degli angoli di vertici 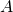 ,
, 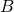 ,
, 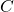 .
.
Enunciamo ora alcuni teoremi fondamentali.
- Teorema dei seni
In un triangolo i lati sono proporzionali ai seni degli angoli rispettivamente opposti ad essi e tale rapporto tra i lati e i seni degli angoli opposti è uguale al diametro della circonferenza circoscritta al triangolo. In formula:
![]()
con ![]() raggio della circonferenza circoscritta al triangolo.
raggio della circonferenza circoscritta al triangolo.
- Teorema della corda
In una circonferenza di raggio ![]() , una corda è uguale al prodotto del diametro per il seno di un angolo alla circonferenza opposto alla corda stessa. In formula:
, una corda è uguale al prodotto del diametro per il seno di un angolo alla circonferenza opposto alla corda stessa. In formula:
![]() .
.
- Teorema delle proiezioni
In un triangolo ogni lato è uguale alla somma dei prodotti di ognuno degli altri due lati per il coseno degli angoli compresi tra questi e il lato considerato. In formule:
![]()
![]()
![]()
- Teorema del coseno o di Carnot
In un triangolo il quadrato di un lato vale la somma dei quadrati degli altri due lati, diminuita del doppio prodotto di questi due lati per il coseno dell’angolo tra essi compreso. In formule:
![]()
![]()
![]()
(Questa pagina è stata visualizzata da 813 persone)