Problema 2.1 Scientifico 2011

0

Sia f la funzione definita sull’insieme R dei numeri reali da

    \[f (x) = (ax + b) e^{-\frac x3} + 3.\]

dove a e b sono due reali che si chiede di determinare sapendo che f ammette un massimo nel punto d’ascissa 4 e che f(0) = 2.

 

Si provi che a=1 e b=-1.

 

Dalla traccia sappiamo che la funzione ammette un massimo nel punto di ascissa 4 e che quindi  f'(4)=0 (per definizione di punto stazionario).

Sappiamo anche che la funzione passa per il punto (0,2).

f'(x)=ae^{-\frac x3}-\frac 13 \left( ax+b \right) e^{ -frac x3}=e^{-\frac x3}\left(a-\frac 13 ax - \frac 13 b \right)=\frac 13e^{-\frac x3}\left(3a-ax- b \right)

Risolviamo quindi:

\begin{cases} f(0)=2 \\ f'(4)=0 \end{cases}

\begin{cases} b+3=2 \\ \frac 13e^{-\frac 43}\left(3a-4a- b \right)=0 \end{cases}

\begin{cases} b=-1 \\ a=-b \end{cases}

\begin{cases} b=-1 \\ a=1 \end{cases}

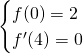
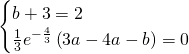
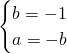
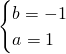
(Questa pagina è stata visualizzata da 8 persone)

Lascia un commento