Problema 2.4 P.N.I. 2014

Sia $f(x)=(2-x) \sqrt{4x-x^2}$

Sia $h(x)= sen(f (x))$ . Quanti sono i punti del grafico di $h(x)$ di ordinata 1? Il grafico di $h(x)$ presenta punti di minimo, assoluti o relativi? Per quali valori reali di k l’equazione $h(x)= k$ ha 4 soluzioni distinte? Qual è il valore di $\int_0^4 h(x) \, dx$ ?

Risposta dello staff

Rendered by QuickLaTeX.com

Analizziamo la funzione $h(x)=sen(f(x))$ :

questa funzione avrà intersezione con gli assi in $O(0;0)$ , $A(2;0)$ e $B(4;0)$ .

Studiamo la derivata prima:

$h'(x)=\frac {2x^2-8x+4}{\sqrt{4x-x^2}} \cdot cos \left( \left(2-x\right) \sqrt{4x-x^2}\right)$

Separando i due fattori, ricaviamo che:

$\frac {2x^2-8x+4}{\sqrt{4x-x^2}} >0 \iff 0<x<2-\sqrt 2 \quad \lor \quad 2+\sqrt 2 <x<4$

$cos \left( \left(2-x\right) \sqrt{4x-x^2}\right) >0 \iff -\frac {\pi}{2}<f(x)<\frac {\pi}{2}$ .

Dal grafico iniziale di $\Gamma$ ricaviamo che:

$f(x)= \frac {\pi}{2}$ per $x=\alpha_1$ con $0<\alpha_1<2-\sqrt 2$ e per $x=\alpha_2$ con $2-\sqrt 2<\alpha_2<2$

$f(x)= -\frac {\pi}{2}$ per $x=\beta_1$ con $2<\beta_1<2+\sqrt 2$ e per $x=\beta_2$ con $2+\sqrt 2<\beta_2<4$ ,

con $\alpha_1$ e $\beta_2$ simmetrici tra loro rispetto a 2, come anche $\alpha_2$ e $\beta_1$ .

Grafico disequazione derivata prima…. l’ordine dei valori è:

$0 - \alpha_1 - 2-\sqrt 2 - \alpha_2 - \beta_1 - 2+\sqrt 2 - \beta_2 - 4$

Con il primo intervallo positivo, e poi alternati!!!

Da qui, ricaviamo che la funzione avrà:

due massimi assoluti in 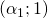$(\alpha_1;1)$ e $(\alpha_2;1)$
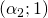
due minimi assoluti in 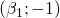$(\beta_1;-1)$ e $(\beta_2;-1)$
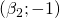
due massimi relativi in 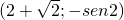$(2+\sqrt 2;-sen 2)$ e $(4;0)$
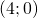
due minimi relativi in 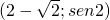$(2-\sqrt 2;sen 2)$ e $(0;0)$

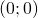
Senza bisogno di tracciare il grafico si deduce che le rette del fascio $y = k$ (parallele all’asse x) intersecano la funzione in quattro punti distinti per i valori di k compresi tra l’ordinata del punto di minimo relativo $(2 − \sqrt 2; sen 2)$ e le ordinate dei punti di massimo assoluto e tra l’ordinata del punto di massimo relativo $(2 + \sqrt 2; − sen 2)$ e le ordinate dei punti di minimo assoluto.