Di sicuro il metodo più semplice dei 4, consiste nel ricavare un’incognita in funzione di un’altra in una delle due equazioni e poi sostituirla nell’altra.
A questo punto, la seconda diventa un’equazione di primo grado in una sola incognita.
Risolta quest’ultima, sostituiamo poi il valore appena trovato nell’equazione inizialmente modificata.
In generale, per i sistemi di 2 equazioni in 2 incognite possiamo sintetizzare il tutto con:
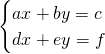
dove ![]() sono termini noti e
sono termini noti e ![]() le incognite,
le incognite,
nella prima equazione troviamo la ![]() e avremo:
e avremo:
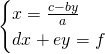
Trovato il valore della ![]() sostituiamo questo valore nella seconda, così da avere:
sostituiamo questo valore nella seconda, così da avere:
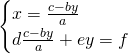
Ora la seconda è un’equazione di primo grado in funzione della sola ![]() .
.
Senza svolgere tutti i calcoli, otteniamo:
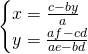 .
.
Trovata la ![]() sostituiamo adesso questo valore, che anche se non sembra, è numerico,nella prima equazione così da trovare il valore della
sostituiamo adesso questo valore, che anche se non sembra, è numerico,nella prima equazione così da trovare il valore della ![]() :
:
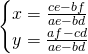 .
.
Volendo, si potrebbe utilizzare sempre questa formula per risolvere tutti i sistemi di equazioni di primo grado in 2 incognite senza fare alcun calcolo.
Altri argomenti simili:
- Esercizi Sistemi equazioni letterali a due incognite
- Metodo di confronto
- Metodo di Cramer
- Metodo di riduzione (o eliminazione)
- Metodo di sostituzione
- Problemi di geometria con due o più incognite
- Problemi di primo grado
- Sistemi che si risolvono con artifici
- Sistemi di equazioni di primo grado a più di due incognite
- Sistemi in cui figurano valori assoluti di espressioni contenenti l’incognita
- Sistemi lineari di due equazioni numeriche in due incognite
(Questa pagina è stata visualizzata da 804 persone)