Problemi di primo grado 5.

Determinare due numeri sapendo che la loro somma è cinque volte la loro differenza e che i $\frac 79$ del maggiore superano di 5 i $\frac 3 4$ del minore.

$\Bigg\{ \begin{array}{l} x+y=5(x-y) \\ \frac 79 x=5+ \frac 3 4 y \end{array}$

$\Bigg\{ \begin{array}{l} x+y=5x-5y \\ \frac {28x-27y} {36}=\frac {180}{5} \end{array}$

$\Bigg\{ \begin{array}{l} x-5x=-y-5y \\ 28x-27y=180 \end{array}$

$\Bigg\{ \begin{array}{l} -4x=-6y \\ 28x-27y=180 \end{array}$

$\Bigg\{ \begin{array}{l} x=\frac 3 2 y \\ 28(\frac3 2 y)-27y=180 \end{array}$

$\Bigg\{ \begin{array}{l} x=\frac 32 y \\ 42y-27y=180 \end{array}$

$\Bigg\{ \begin{array}{l} x=\frac 32 y \\ 15y=180 \end{array}$

$\Bigg\{ \begin{array}{l} x=\frac 32 y \\ y=\frac {180}{15}=12 \end{array}$

$\Bigg\{ \begin{array}{l} x=\frac 32 12=18 \\ y= 12 \end{array}$

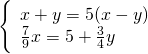
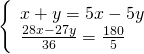
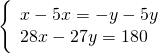
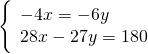
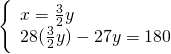
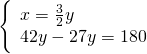
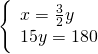
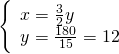
Altri hanno visualizzato:

Problemi di primo grado 1
Problemi di primo grado 2
Problemi di primo grado 3
Problemi di primo grado 4
Problemi di primo grado 5

(Questa pagina è stata visualizzata da 250 persone)

Matebook

La matematica spiegata passo passo

Problemi di primo grado 5

Lascia un commento Annulla risposta