Traccia
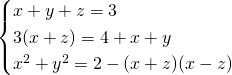
Svolgimento
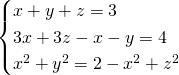
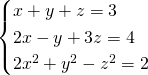
Il nostro scopo iniziale è quello di risolvere l’equazione di secondo grado, quindi usiamo il metodo di sostituzione nelle altre 2 equazioni, e sfruttiamo i risultati per la terza.
In questo caso se facciamo la somma tra le prime due otteniamo:
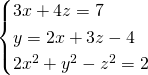
Dalla prima ricaviamo la ![]() , così da poterci poi calcolare le due triple di risultati:
, così da poterci poi calcolare le due triple di risultati:
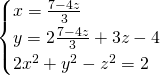
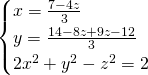
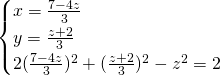
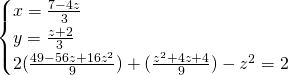
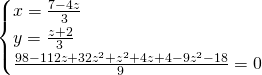
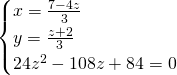
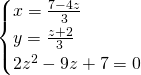
La terza equazione è un trinomio speciale, e ammetterà come soluzioni:
![]()
da cui
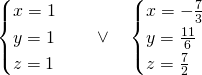
Altri esercizi simili
- Esercizio 1 Sistemi di equazioni di grado superiore al primo: 3 equazioni in 3 incognite
- Esercizio 2 Sistemi di equazioni di grado superiore al primo: 3 equazioni in 3 incognite
- Esercizio 3 Sistemi di equazioni di grado superiore al primo: 3 equazioni in 3 incognite
- Esercizio 4 Sistemi di equazioni di grado superiore al primo: 3 equazioni in 3 incognite
- Esercizio 5 Sistemi di equazioni di grado superiore al primo: 3 equazioni in 3 incognite
(Questa pagina è stata visualizzata da 289 persone)