Giuseppe scrive: Esercizio sul principio di induzione

Oggetto: SOLUZIONE DI UN ESERCIZIO

Corpo del messaggio:

DIMOSTARE CON IL PRINCIPIO DI INDUZIONE : 2 ^n maggiore di n^2 con n maggiore e uguale a 4

$2^4=16 \geq 4^2 =16$
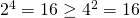
Supponiamo vero che 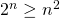$2^n \geq n^2$ , allora si dovrebbe verificare che 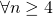$\forall n \geq 4$ sia:

$2^{n+1}\geq (n+1)^2$

$2 \cdot 2^n \geq n^2+2n+1$

$2^n\geq \frac {n^2+2n+1}{2}$

Sappiamo per hp che $2^n>n^2$ , per $n\geq 4$ .

Verifichiamo quindi che:

$n^2 \geq \frac {n^2+2n+1}{2}$ con $n\geq 4$ .

$2n^2 \geq n^2+2n+1$

$n^2-2n \geq 1$

che è sempre verificato $\forall n >2$ .

cvd…

(Questa pagina è stata visualizzata da 72 persone)

Matebook