Leandro scrive: Esercizi sulla retta

Pubblicato il da Lo Staff2 commenti
0

Oggetto: Esercizi sulla retta

Corpo del messaggio:
img058

 

 

1) Il triangolo sarà formato dall’origine e dai due punti di intersezione della retta con gli assi cartesiani.

I tre punti avranno quindi coordinate:

O(0;0)

A(0;2)

B(\frac{2}{a+3};0)

Affinchè l’area sia uguale ad \frac 14, avremo:

\frac {2 \cdot \left| \frac {2}{a+3} \right|}{2}=\frac 14

\left| \frac {2}{a+3} \right|=\frac 14

Studiamo separatamente i due casi:

  • \frac {2}{a+3} =\frac 14

a+3=8

a=5

  • \frac {2}{a+3} =-\frac 14

a+3=-8

a=-11

Ambedue le soluzioni sono accettabili.

2)Ricaviamo le coordinate dei punti:

  • \begin{cases} x-y-4=0\\x+y-2=0 \end{cases}

\begin{cases} y=x-4\2x=6 \end{cases}

\begin{cases} y=-1\\ x=3 \end{cases}

  • \begin{cases} x-y-4=0\\x+y-6=0 \end{cases}

\begin{cases} y=x-4\\2x=10 \end{cases}

\begin{cases} y=1\\ x=5 \end{cases}

  • \begin{cases} x-y=0\\x+y-2=0 \end{cases}

\begin{cases} x=y\\2y=2 \end{cases}

\begin{cases} x=1\\ y=1 \end{cases}

  • \begin{cases} x-y=0\\x+y-6=0 \end{cases}

\begin{cases} x=y\\2y=6 \end{cases}

\begin{cases} x=3\\ y=3 \end{cases}

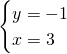
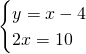
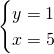
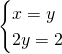
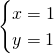
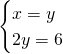
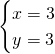
Verifichiamo sia un quadrato:

AB=\sqrt{(3-1)^2+(3-1)^2}=\sqrt{4+4}=\sqrt 8

BC=\sqrt{(3-5)^2+(3-1)^2}=\sqrt{4+4}=\sqrt 8

CD=\sqrt{(5-3)^2+(1+1)^2}=\sqrt{4+4}=\sqrt 8

AD=\sqrt{(1-3)^2+(1+1)^2}=\sqrt{4+4}=\sqrt 8

Il quadrilatero è proprio un quadrato.

3)

a) m(x-2)+y+1=0

Quindi il centro avrà coordinate C(2:-1)

b) m(6x-10)-6y+3=0

Quindi il centro avrà coordinate C(\frac 53:\frac 12)

c) 3y+2-mx=0

Quindi il centro avrà coordinate C(0:-\frac 23)

d) 2k(3x+5)-3y=0

Quindi il centro avrà coordinate C(-\frac 53:0)

e) m(x-6)+3y+3=0

Quindi il centro avrà coordinate C(6:-1)

f) 5m(1-x)+5y+2=0

Quindi il centro avrà coordinate C(1:-\frac 25)

(Questa pagina è stata visualizzata da 168 persone)

2 pensieri riguardo “Leandro scrive: Esercizi sulla retta”

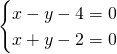
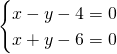
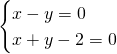
  1. In merito all’esercizio n.1, le due soluzioni sono accettabili in quanto sono tutte e due diverse dal valore che annulla il denominatore cioè a diverso da -3. E’ giusto?
    In merito all’esercizio n.2, per verificare che il quadrilatero ABCD è un quadrato si è verificato naturalmente che i lati formano quattro angoli retti e non solo che essi sono congruenti. Giusto?

    Grazie

    1. Sull’esercizio 1 è esattamente come dici tu.
      Sull’esercizio 2 le due rette sono chiaramente perpendicolari, in quanto i loro coefficienti angolari sono 1 e -1, e lo avevo dato per scontato.

Lascia un commento