Si consideri una funzione
![]()
razionale fratta, ovverio il quoziente di due polinomi ![]() di grado
di grado ![]() e
e ![]() di grado
di grado ![]() . Se
. Se ![]() , si può effettuare la divisione tra il polinomio al numeratore
, si può effettuare la divisione tra il polinomio al numeratore ![]() e il polinomio a denominatore
e il polinomio a denominatore ![]() , ricavando come quoziente un polinomio
, ricavando come quoziente un polinomio ![]() di grado
di grado ![]() e come resto un polinomio
e come resto un polinomio ![]() di grado
di grado ![]() .
.
La funzione ![]() si può quindi scrivere nella forma:
si può quindi scrivere nella forma:
![]() .
.
In tal caso, quindi, calcolare ![]() equivale a calcolare
equivale a calcolare
![]() .
.
Il primo integrale ![]() è facilmente calcolabile poichè la funzione
è facilmente calcolabile poichè la funzione ![]() è un polinomio, mentre il secondo integrale
è un polinomio, mentre il secondo integrale ![]() richiede l’applicazione del criterio relativo all’integrazione delle funzioni razionali fratte, il cui numeratore è un polinomio di grado inferiore al grado del polinomio a denominatore.
richiede l’applicazione del criterio relativo all’integrazione delle funzioni razionali fratte, il cui numeratore è un polinomio di grado inferiore al grado del polinomio a denominatore.
A tal scopo vengono presentati i casi più significativi e ricorrenti:
a) il polinomio a denominatore è di primo grado o una sua potenza naturale.
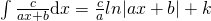 , con
, con 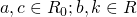 ;
;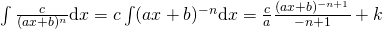 , con
, con 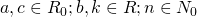 ;
;
b) il polinomio a denominatore è di secondo grado, ![]() . L’integrale ha un’espressione del tipo.
. L’integrale ha un’espressione del tipo.
![]() non contemporaneamente nulli.
non contemporaneamente nulli.
In tal caso occorre fare un’ulteriore distinzione, a seconda del discriminante ![]() del polinomio a denominatore:
del polinomio a denominatore:
c) Il polinomio a denominatore è di grado superiore al secondo. In tal caso occorre fare un’ulteriore distinzione.
- Il polinomio
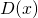 a denominatore, di grado
a denominatore, di grado 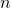 , con
, con 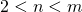 ammette
ammette 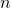 soluzioni reali e distinte, ovvero di molteplicità 1,
soluzioni reali e distinte, ovvero di molteplicità 1, 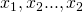 , e quindi risulta scomponibile nella forma
, e quindi risulta scomponibile nella forma 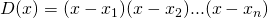 . La funzione integranda può essere decomposta nella somma di
. La funzione integranda può essere decomposta nella somma di 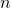 frazioni elementari:
frazioni elementari:
![]() ,
,
ove ![]() sono costanti reali da determinare applicando il principio di identità dei polinomi, per cui il criterio per il calcolo dell’integrale è analogo a quello descritto nel caso
sono costanti reali da determinare applicando il principio di identità dei polinomi, per cui il criterio per il calcolo dell’integrale è analogo a quello descritto nel caso ![]() .
.
- Il polinomio
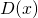 a denominatore, di grado
a denominatore, di grado 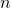 ,
, 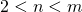 , ammette soluzioni reali anche di molteplicità maggiore di 1; ad esempio, risulta scomponibile nella forma
, ammette soluzioni reali anche di molteplicità maggiore di 1; ad esempio, risulta scomponibile nella forma 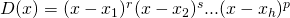 , dove
, dove  . La funzione integranda può essere decomposta nella somma di frazioni elementari:
. La funzione integranda può essere decomposta nella somma di frazioni elementari:
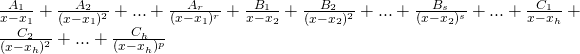 ,
,
con ![]() costanti reali da determinare applicando il principio di identità dei polinomi, e il criterio per il calcolo dell’integrale è una generalizzazione di quello descritto nel caso
costanti reali da determinare applicando il principio di identità dei polinomi, e il criterio per il calcolo dell’integrale è una generalizzazione di quello descritto nel caso ![]() .
.
- Il polinomio
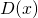 a denominatore, di grado
a denominatore, di grado 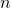 ,
, 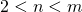 , ammette, oltre a soluzioni reali, anche zeri complessi di molteplicità 1. In tal caso la funzione integranda può essere decomposta nella somma di frazioni in modo che il numeratore delle frazioni, con denominatore un polinomio di secondo grado a zeri complessi, sia un polinomio di primo grado. Il calcolo dei corrispondenti integrali segue i criteri precedentemente descritti.
, ammette, oltre a soluzioni reali, anche zeri complessi di molteplicità 1. In tal caso la funzione integranda può essere decomposta nella somma di frazioni in modo che il numeratore delle frazioni, con denominatore un polinomio di secondo grado a zeri complessi, sia un polinomio di primo grado. Il calcolo dei corrispondenti integrali segue i criteri precedentemente descritti.
Altri hanno visualizzato anche
[siblings depth=1]
(Questa pagina è stata visualizzata da 1026 persone)