Geometria del piano

Richiami di teoria di geometria piana

Criteri di congruenza dei triangoli

Primo criterio: due triangoli sono congruenti se hanno rispettivamente congruenti due lati e l’angolo compreso.
Secondo criterio: due triangoli sono congruenti se hanno rispettivamente congruenti un lato e i due angoli adiacenti.
Terzo criterio: due triangoli sono congruenti se hanno rispettivamente congruenti i tre lati.

Criteri di congruenza dei triangoli nel caso particolare dei triangoli rettangoli

Due triangoli rettangoli sono congruenti se hanno rispettivamente congruenti un lato e un angolo.
Due triangoli rettangoli sono congruenti se hanno rispettivamente congruenti due lati.

Rette parallele

Due rette parallele tagliate da una trasversale formano:

angoli alterni interni congruenti;
angoli alterni esterni congruenti;
angoli corrispondenti congruenti;
angoli coniugati interni supplementari;
angoli coniugati esterni supplementari; e viceversa.

Punti notevoli di un triangolo

Dato un triangolo, si dice:

baricentro il punto di incontro delle mediane;
circocentro il punto di incontro degli assi;
incentro il punto di incontro delle bisettrici;
ortocentro il punto di incontro delle altezze.

Parallelogrammi

Si dice parallelogramma un quadrilatero che ha i lati opposti paralleli tra loro.

Se un quadrilatero è un parallelogramma, allora:

gli angoli opposti sono congruenti;
gli angoli adiacenti a uno stesso lato sono supplementari;
le diagonali si tagliano scambievolmente per metà; e viceversa.
Si dice rettangolo un parallelogramma con tutti gli angoli retti.
Si dice rombo un parallelogramma con tutti i lati congruenti.
Si dice quadrato un quadrilatero che ha tutti i lati congruenti e tutti gli angoli retti.

Circonferenza

Si dice circonferenza il luogo geometrico di punti del piano equidistanti $r$ (raggio) da un punto detto centro; cerchio i punti interni alla circonferenza e la circonferenza stessa.

Si dice corda un segmento congiungente due punti della circonferenza.

Si dice diametro una corda passante per il centro.

Si dicono settori circolari le due parti nelle quali un cerchio viene diviso da due suoi raggi.

Si dicono segmenti circolari le due parti nelle quali un cerchio viene diviso da una sua corda.

Data una retta complanare con una circonferenza, si dice:

secante la retta che taglia la circonferenza in due punti distinti;
tangente la retta che ha un solo punto d’intersezione con la circonferenza (ovvero due punti coincidenti);
esterna una retta che non ha punti di intersezione con la circonferenza.

Una retta tangente è sempre perpendicolare al raggio condotto per il suo punto di tangenza.

Si dice angolo alla circonferenza un angolo che ha il vertice sulla circonferenza e i lati ambedue secanti, oppure uno secante e uno tangente la circonferenza.

Si dice angolo al centro un angolo che ha il vertice nel centro della circonferenza e per lati due raggi uscenti dal centro.

Un angolo al centro è sempre doppio di un angolo alla circonferenza che insiste sulla stessa corda (o sullo stesso arco).

Tutti gli angoli alla circonferenza che insistono su una stessa corda (o arco), e che si trovano dalla stessa parte rispetto a essa, sono tra loro congruenti.

I triangoli che hanno come lato un diametro e un vertice sulla circonferenza sono rettangoli.

Un quadrilatero è inscrittibile in una circonferenza quando la somma degli angoli opposti è un angolo piatto, e viceversa.

Un quadrilatero è circoscrittibile a un circonferenza quando le somme dei lati opposti sono congruenti, e viceversa.

Disuguaglianza triangolare

In un triangolo un lato è sempre maggiore della differenza degli altri due ed è sempre 38 minore della loro somma.

Teoremi di Euclide

In un triangolo rettangolo il quadrato costruito su un cateto è equivalente al rettangolo che ha per dimensioni l’ipotenusa e la proiezione del cateto sull’ipotenusa; oppure, in modo equivalente, il cateto è medio proporzionale tra l’ipotenusa e la sua proiezione sull’ipotenusa.
In un triangolo rettangolo il quadrato costruito sull’altezza relativa all’ipotenusa è equivalente al rettangolo che ha per dimensioni le due proiezioni dei cateti sull’ipotenusa; oppure, in modo equivalente, l’altezza relativa all’ipotenusa è media proporzionale tra le proiezioni dei cateti sull’ipotenusa.

Teorema di Pitagora

Il quadrato costruito sull’ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti.

Similitudine tra triangoli

Due triangoli si dicono simili se hanno gli angoli rispettivamente congruenti e i lati corrispondenti in proporzione. Il rapporto tra lati corrispondenti si dice rapporto di similitudine.

Primo criterio di similitudine: se due triangoli hanno due angoli rispettivamente congruenti, sono simili.
Secondo criterio di similitudine: se due triangoli hanno due lati in proporzione e l’angolo compreso di eguale ampiezza, congruente, sono simili.
Terzo criterio di similitudine: se due triangoli hanno i tre lati in proporzione, sono simili.

I perimetri di triangoli simili hanno rapporto uguale al valore assoluto del rapporto di similitudine.

Le aree di triangoli simili hanno rapporto uguale al quadrato del rapporto di similitudine.

Aree di figure piane

Triangolo: 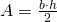$A=\frac {b \cdot h }{2}$ , dove 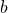$b$ è la base e 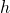$h$ l’altezza.
Rettangolo o parallelogramma: 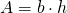$A=b \cdot h$ , dove 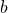$b$ è la base e 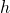$h$ l’altezza.
Trapezio: 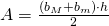$A=\frac {(b_M+b_m)\cdot h}{2}$ , dove 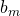$b_m$ è la base minore 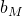$b_M$ è la base maggiore e 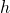$h$ l’altezza.
Cerchio: 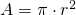$A=\pi \cdot r^2$ , dove $r$ è il raggio.
Superficie della sfera: 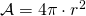$\mathcal {A}= 4 \pi \cdot r^2$ , dove $r$ è il raggio.