- Di un triangolo ABC, isoscele sulla base AB, si sa che il rapporto tra AC e AB è
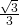 . Determinare gli angolo del triangolo.
. Determinare gli angolo del triangolo. - In un triangolo isoscele circoscritto ad un cerchio di raggio r, il rapporto tra l’altezza relativa alla base e la base è
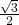 . Trovare il perimetro e l’area del triangolo
. Trovare il perimetro e l’area del triangolo - In un triangolo isoscele inscritto in una circonferenza di raggio r, la somma del doppio dell’altezza con il triplo del lato è
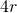 . Determinare l’ampiezza dell’angolo al vertice.
. Determinare l’ampiezza dell’angolo al vertice. - Determinare l’area di un parallelogramma di cui si conoscono due lati consecutivi (cm 8 e cm 6) e l’ampiezza dell’angolo compreso (
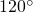 )
) - In un quadrato ABCD si consideri sul lato AD il punto M tale che
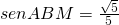 e sul lato CD il punto N tale che
e sul lato CD il punto N tale che 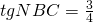 . Sapendo che il lato del quadrato ha per misura 8, si trovino:
. Sapendo che il lato del quadrato ha per misura 8, si trovino:
Altri esercizi simili
- Problema di geometria piana risolubili con l’uso della trigonometria
- Problemi relativi alla circonferenza, ai triangoli e ai quadrilateri inscritti e circoscritti
(Questa pagina è stata visualizzata da 292 persone)
Un pensiero riguardo “Problema di geometria piana risolubili con l’uso della trigonometria”