Tracce
- In una circonferenza di centro
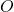 è data una corda
è data una corda 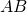 congruente agli
congruente agli 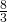 della sua distanza dal centro; si sa inoltre che, detta
della sua distanza dal centro; si sa inoltre che, detta 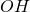 tale distanza, è verificata la relazione
tale distanza, è verificata la relazione
![Rendered by QuickLaTeX.com \[\frac 56 AH + \frac 49 OH =14 dm\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-b07e9c53865d89604752d19810036394_l3.png)
. Determinare il raggio della circonferenza.
- Il lato di un rombo supera di 2 m la metà della diagonale maggiore e la somma del lato e della diagonale maggiore è 26 m. Determinare le lunghezze delle diagonali e del raggio della circonferenza inscritta.
- In una circonferenza di diamtro
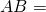 30 cm è data una corda
30 cm è data una corda 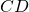 perpendicolare nel punto
perpendicolare nel punto 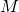 al diametro
al diametro 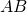 . Sapendo che
. Sapendo che
![Rendered by QuickLaTeX.com \[\frac 34 AM + \frac 13 MB=20 cm\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-8163df7b9156164fde0f0a322ad1223c_l3.png)
, determinare l’area del quadrilatero
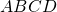 . (Porre
. (Porre 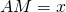 ).
). - E’ data una circonferenza di centro
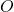 e di diametro
e di diametro 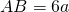 ; si prolunghi il diametro
; si prolunghi il diametro 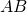 , oltre
, oltre 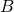 , di un segmento
, di un segmento 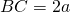 e da
e da 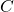 si conducano le due tangenti alla circonferenza. Detti
si conducano le due tangenti alla circonferenza. Detti 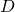 ed
ed 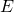 i due punti di contatto, si determini il segmento
i due punti di contatto, si determini il segmento 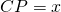 , su
, su 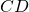 , in modo che sia verificata la seguente relazione:
, in modo che sia verificata la seguente relazione:
![Rendered by QuickLaTeX.com \[\frac 34 CE - 2PC = \frac 13 PD\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-273a2102250d77289e61ae7bab142dc8_l3.png)
. Determinare, poi, il perimetro e l’area del quadrilatero
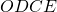 .
. - Nella semicirconferenza di diametro
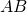 è inscritto il triangolo
è inscritto il triangolo 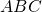 del quale si conosce che
del quale si conosce che
![Rendered by QuickLaTeX.com \[AC \cong \frac 43 BC \quad \mbox { e } \quad \frac {AC}{6} - \frac {CB}{12}=5 \mbox{ cm }\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-9ddadcff66efeecb0c558b56b5c440cb_l3.png)
. Determinare il diametro
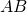 , il perimetro e l’area del triangolo ABC.
, il perimetro e l’area del triangolo ABC. - Un trapezio isoscele è circoscritto a una semicirconferenza di diametro 30 cm. Dopo aver dimostrato che il lato obliquo è metà della base maggiore, determinare il perimetro del trapezio sapendo che il diametro è il triplo della base minore.
- Un trapezio isoscele di perimetro 110 cm è circoscritto a una semicirconferenza. Dopo aver dimostrato che il lato obliquo è congruente a metà della base maggiore,, determinare i lati del trapezio sapendo che la base minore è i
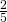 del lato obliquo. Determinare inoltre l’area del trapezio.
del lato obliquo. Determinare inoltre l’area del trapezio. - In una circonferenza di centro
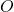 è data una corda
è data una corda 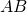 che è gli
che è gli 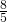 del raggio; i sa inoltre che
del raggio; i sa inoltre che 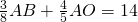 cm. Determinare l’area del triangolo isoscele
cm. Determinare l’area del triangolo isoscele 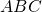 inscritto nella circonferenza contenente il centro e avente per base la corda
inscritto nella circonferenza contenente il centro e avente per base la corda 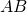 .
. - Nel triangolo isoscele
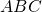 , la base
, la base 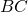 è congruente all’altezza
è congruente all’altezza 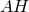 a essa relativa: si sa, inoltre che la differenza fra i
a essa relativa: si sa, inoltre che la differenza fra i 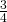 di
di 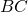 e i
e i 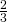 di
di 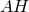 è 4 cm. Determinare il diametro della circonferenza circoscritta al triangolo.
è 4 cm. Determinare il diametro della circonferenza circoscritta al triangolo. - In un triangolo isoscele la base supera il lato di
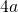 e la somma della metà della base e dei
e la somma della metà della base e dei 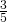 del lato è congruente alla base stessa. Determinare il diametro della circonferenza circoscritta.
del lato è congruente alla base stessa. Determinare il diametro della circonferenza circoscritta. - In un trapezio isoscele la base minore è i
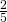 del lato obliquo, il perimetro è 80 cm e la somma della quarta parte della base maggiore con la metà della base minore è 12 cm. Verificare che il trapezio è circoscrivibile a una circonferenza e calcolarne il diametro,
del lato obliquo, il perimetro è 80 cm e la somma della quarta parte della base maggiore con la metà della base minore è 12 cm. Verificare che il trapezio è circoscrivibile a una circonferenza e calcolarne il diametro, - Un triangolo isoscele
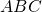 , di base
, di base 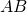 e altezza
e altezza 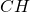 , è inscritto in una circonferenza di centro
, è inscritto in una circonferenza di centro 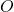 . Sapendo che
. Sapendo che
![Rendered by QuickLaTeX.com \[\frac 29 CH + \frac 16 AB=CH-AB=3 \mbox{ cm }\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-83b2a3de6bee2dc400b6ca1751dcf194_l3.png)
, si verifichi che la distanza tra
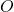 e i lati congruenti +
e i lati congruenti + 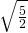 cm.
cm. - Il quadrilatero
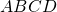 ha la diagonale maggiore
ha la diagonale maggiore 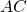 perpendicolarae alla diagonale minore
perpendicolarae alla diagonale minore 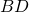 nel suo punto medio
nel suo punto medio 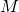 . Determinare le lunghezze delle diagonali sapendo che la loro somma è 49 m e che la differenza tra i
. Determinare le lunghezze delle diagonali sapendo che la loro somma è 49 m e che la differenza tra i 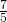 della maggiore e i
della maggiore e i 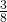 della minore è 26 m. Sapendo inoltre che
della minore è 26 m. Sapendo inoltre che 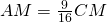 , determinare le lunghezze dei lati del quadrilatero e verificare che gli angoli in
, determinare le lunghezze dei lati del quadrilatero e verificare che gli angoli in 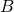 e in
e in 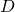 sono retti. Dopo aver dimostrato che il quadrilatero è circoscrivibile a una circonferenza, determinare il raggio della circonferenza inscritta.
sono retti. Dopo aver dimostrato che il quadrilatero è circoscrivibile a una circonferenza, determinare il raggio della circonferenza inscritta. - Un trapezio
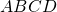 è circoscritto ad una circonferenza ed è
è circoscritto ad una circonferenza ed è 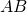 la base maggiore,
la base maggiore, 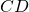 la base minore,
la base minore, 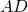 il lato obliquo minore. Si sa che
il lato obliquo minore. Si sa che
![Rendered by QuickLaTeX.com \[\frac 25 AB + \frac 23 AD=88 \mbox{ cm } \quad CB-CD= 6 \mbox{ dm } \quad \mbox { e } \quad AD+BC=14 \mbox { dm}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-1b873fb4a13181686e785c54645324a0_l3.png)
. Determinare i lati del trapezio e, successivamente, l’area. (Porre
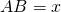 e
e 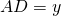 ).
). - In un triangolo rettangolo la somma dei
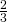 del cateto minore e dei
del cateto minore e dei 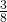 del maggiore è 21 cm e la differenza delle lunghezze dei cateti è 6 cm. determinare la lunghezza del raggio della circonferenza inscritta dopo aver dimostrato che la somma dei cateti supera l’ipotenusa di un segmento avente la lunghezza del diametro della circonferenza inscritta.
del maggiore è 21 cm e la differenza delle lunghezze dei cateti è 6 cm. determinare la lunghezza del raggio della circonferenza inscritta dopo aver dimostrato che la somma dei cateti supera l’ipotenusa di un segmento avente la lunghezza del diametro della circonferenza inscritta. - I triangoli isosceli
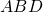 e
e 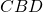 hanno in comune la base
hanno in comune la base 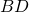 e i vertici
e i vertici 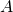 e
e 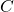 giacciono da parte opposta rispetto alla base
giacciono da parte opposta rispetto alla base 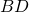 . Le misure dei perimetri dei triangoli sono rispettivamente
. Le misure dei perimetri dei triangoli sono rispettivamente 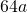 e
e 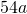 . Determinare le misure dei lati dei triangoli sapendo che:
. Determinare le misure dei lati dei triangoli sapendo che:
![Rendered by QuickLaTeX.com \[\frac 45 BC - \frac 14 AB = 7a\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-58c575c620e5120122b341e4c3a0c9d8_l3.png)
Verificare che gli angoli in
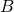 e in
e in 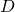 del quadrilatero
del quadrilatero 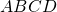 sono retti e determinare la misura del raggio della circonferenza circoscritta la quadrilatero.
sono retti e determinare la misura del raggio della circonferenza circoscritta la quadrilatero. - Il perimetro di un triangolo isoscele è 128 m e i 3/4 del lato superano di 15 m i
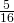 della base. Determinare le lunghezze dei raggi della circonferenza inscritta e della circonferenza circoscritta
della base. Determinare le lunghezze dei raggi della circonferenza inscritta e della circonferenza circoscritta - In una circonferenza di centro
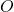 è inscritto il triangolo isoscele
è inscritto il triangolo isoscele 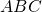 , di base
, di base 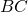 e la cui altezza relativa alla base è
e la cui altezza relativa alla base è 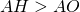 . Si sa che sono verificate le seguenti relazioni:
. Si sa che sono verificate le seguenti relazioni:
![Rendered by QuickLaTeX.com \[\frac 14 AH + \frac 25 BO=9 \mbox { cm }; \quad AO-OH=9 \mbox { cm }\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-e3c299b857de10196d59d70fe3b48a9b_l3.png)
.Determinare il perimetro del triangolo e la sua area.
- Il trapezio
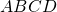 è circoscritto ad una circonferenza;la base maggiore
è circoscritto ad una circonferenza;la base maggiore 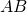 è il doppio del lato obliquo
è il doppio del lato obliquo 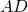 ed i
ed i 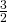 dell’altro lato obliquo
dell’altro lato obliquo 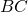 . Determinare il perimetro del trapezio sapendo che la somma dei
. Determinare il perimetro del trapezio sapendo che la somma dei 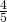 della base minore
della base minore 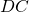 e del lato obliquo maggiore
e del lato obliquo maggiore 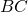 è 38 cm.
è 38 cm. - Nel triangolo
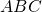 i lati
i lati 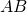 e
e 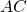 superano rispettivamente di 28 cm e 8 cm le loro proiezioni
superano rispettivamente di 28 cm e 8 cm le loro proiezioni 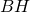 e
e 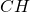 sul lato
sul lato 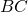 . Si conosce il perimetro del triangolo, 504 cm, e si chiede di determinare i lati del triangolo, l’altezza
. Si conosce il perimetro del triangolo, 504 cm, e si chiede di determinare i lati del triangolo, l’altezza 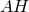 , l’area del triangolo e il raggio del cerchio inscritto nel triangolo.
, l’area del triangolo e il raggio del cerchio inscritto nel triangolo. - Le diagonali del quadrilatero
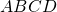 sono perpendicolari e si incontrano in
sono perpendicolari e si incontrano in 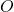 punto medio della diagonale
punto medio della diagonale 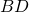 . Determinare i lati del quadrilatero sapendo che il suo perimetro è di 84 cm e che
. Determinare i lati del quadrilatero sapendo che il suo perimetro è di 84 cm e che
![Rendered by QuickLaTeX.com \[\frac 12 DC+\frac 23 AD=24 \mbox { cm }\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-8c98126c30c6262be4a0854abc09a2d1_l3.png)
Dimostrare poi che il quadrilatero è circoscrivibile a una circonferenza e, sapendo che gli angoli
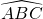 e
e 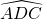 sono retti, calcolare il raggio della circonferenza inscritta.
sono retti, calcolare il raggio della circonferenza inscritta. - Un triangolo isoscele è inscritto in una circonferenza e il centro della circonferenza è interno al triangolo; sommando i
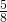 della base a
della base a 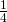 dell’altezza relativa si ottengono 19 cm e la base supera di 12 cm i
dell’altezza relativa si ottengono 19 cm e la base supera di 12 cm i 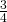 dell’altezza. Determinare le lunghezze dei lati del triangolo e del raggio della circonferenza.
dell’altezza. Determinare le lunghezze dei lati del triangolo e del raggio della circonferenza. - in un triangolo rettangolo la somma dei
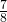 del cateto maggiore e dei
del cateto maggiore e dei 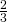 del cateto minore è
del cateto minore è 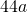 ; sottraendo ai
; sottraendo ai 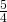 del cateto minore i
del cateto minore i 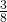 del cateto maggiore si ottiene
del cateto maggiore si ottiene 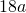 . Determinare le lunghezze dei lati del triangolo e del raggio della circonferenza inscrittta dopo aver dimostrato che il diametro della circonferenza inscritta è congruente alla differenza tra la somma dei cateti e l’ipotenusa.
. Determinare le lunghezze dei lati del triangolo e del raggio della circonferenza inscrittta dopo aver dimostrato che il diametro della circonferenza inscritta è congruente alla differenza tra la somma dei cateti e l’ipotenusa. - Il diametro
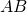 di una circonferenza, lungo 25 cm è diviso dal punto
di una circonferenza, lungo 25 cm è diviso dal punto 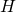 nelle due parti
nelle due parti 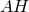 e
e 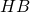 in modo che
in modo che
![Rendered by QuickLaTeX.com \[\frac 14 HB+\frac 13AH=7\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-819045fbda1de8c9a880f7846d8bf402_l3.png)
. Condotta per
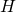 la corda
la corda 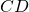 perpendicolare al diametro
perpendicolare al diametro 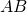 , determinare la lunghezza del perimetro del quadrilatero
, determinare la lunghezza del perimetro del quadrilatero 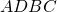 e, dopo aver dimostrato che il quadrilatero è circoscrivibile a una circonferenza, determinare la lunghezza del raggio della circonferenza inscritta.
e, dopo aver dimostrato che il quadrilatero è circoscrivibile a una circonferenza, determinare la lunghezza del raggio della circonferenza inscritta. - Nel triangolo
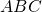 , rettangolo in
, rettangolo in 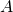 , il cateto minore
, il cateto minore 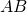 è lungo
è lungo 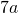 e l’ipotenusa supera di
e l’ipotenusa supera di  l’altro cateto. Determinare sull’ipotenusa
l’altro cateto. Determinare sull’ipotenusa 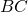 un punto
un punto 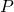 in modo che sia
in modo che sia
![Rendered by QuickLaTeX.com \[\frac 14 BP+\frac 13 CP \cong AB\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-ddb43cbdf0d67352351a729cf5db0644_l3.png)
.
Condotta la circonferenza circoscritta al triangolo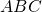 , sia
, sia 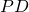 la semicorda, esterna al triangolo
la semicorda, esterna al triangolo 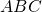 , perpendicolare a
, perpendicolare a 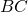 . Determinare la lunghezza del perimetro e l’area del quadrilatero
. Determinare la lunghezza del perimetro e l’area del quadrilatero 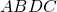 .
. - E’ data una semicirconferenza di diametro
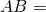 12 cm; il punto
12 cm; il punto 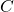 divide
divide 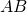 in parti proporzionali ai numeri 1 e 4. Si conduca da
in parti proporzionali ai numeri 1 e 4. Si conduca da 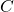 la perpendicolare ad
la perpendicolare ad 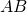 che incontri in
che incontri in 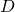 la semicirconferenza e, dopo aver determinato
la semicirconferenza e, dopo aver determinato 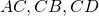 , si determini sull’arco
, si determini sull’arco 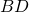 un punto
un punto 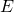 in modo che si abbia
in modo che si abbia
![Rendered by QuickLaTeX.com \[\frac 19 EH + \frac 14 EK = 2 \mbox { cm} \quad \mbox { e } \quad \frac 15 DH + \frac 12 BK = 1,2 \mbox { cm }.\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-fafeded975df2e81d5ec7ce498b5e8e0_l3.png)
, essendo
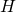 e
e 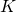 le proiezioni ortogonali di
le proiezioni ortogonali di 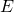 rispettivamente su
rispettivamente su 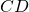 e
e 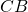 . Come risulta il quadrilatero
. Come risulta il quadrilatero 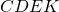 ?
?
Altri esercizi simili:
- Problema di geometria piana risolubili con l’uso della trigonometria
- Problemi relativi alla circonferenza, ai triangoli e ai quadrilateri inscritti e circoscritti
(Questa pagina è stata visualizzata da 545 persone)