Esercizio 24 Problemi di geometria

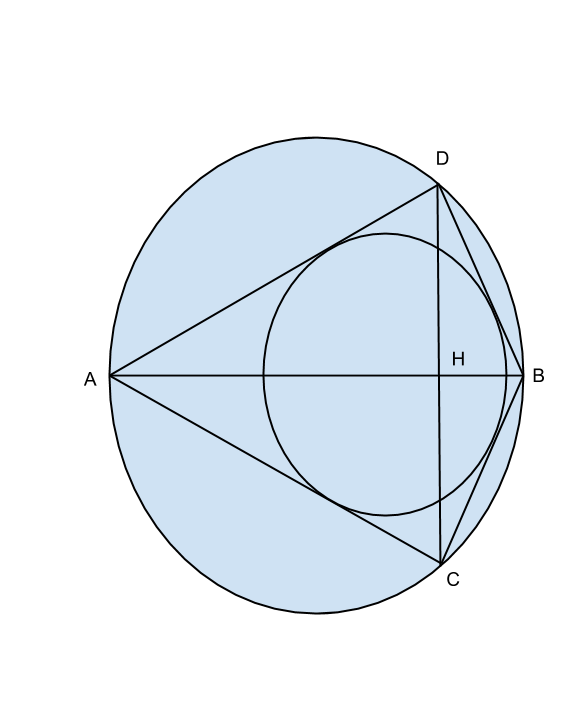
Traccia

Il diametro $AB$ di una circonferenza, lungo 25 cm è diviso dal punto $H$ nelle due parti $AH$ e $HB$ in modo che

$\frac 14 HB+\frac 13AH=7$

. Condotta per $H$ la corda $CD$ perpendicolare al diametro $AB$ , determinare la lunghezza del perimetro del quadrilatero $ADBC$ e, dopo aver dimostrato che il quadrilatero è circoscrivibile a una circonferenza, determinare la lunghezza del raggio della circonferenza inscritta.

Svolgimento

Ricaviamo subito i due segmenti $AH=x$ e $BH=y$ :

$\begin{cases} x+y=25 \\ \frac 14 y + \frac 13 x =7 \end{cases}$

$\begin{cases} x+y=25 \\ \3 y +4 x =84 \end{cases}$

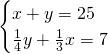
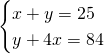
Applichiamo il metodo di riduzione, moltiplicando la prima equazione per 3 e sottraendo membro a membro:

$\begin{cases} x+y=25 \\ \3x+3y-3 y -4 x =75-84 \end{cases}$

$\begin{cases} x+y=25 \\ \- x =-9 \end{cases}$

$\begin{cases} y=16 \\ \ x =9 \end{cases}$ .

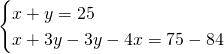
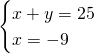
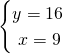Quindi:

$AH= 9 \mbox { cm}$

$BH= 16 \mbox { cm}$

Per costruzione, avremo che $CH=HD$ , essendo CD una corda perpendicolare al diametro e i due triangoli ABC e ADB, ambedue rettangoli, sono congruenti.

Troviamo quindi AC e BC con Euclide:

$AC=\sqrt {AH \cdot AB}=\sqrt {9 \cdot 25}\mbox { cm}=15\mbox { cm}$

$BC=\sqrt {BH \cdot AB}=\sqrt {16 \cdot 25}\mbox { cm}=20\mbox { cm}$ .

Di conseguenza avremo anche:

$AC=AD=15\mbox { cm}$

$BC=BD=20\mbox { cm}$

Il perimetro del quadrilatero sarà:

$2p_{ABCD}=(20+15+15+20)\mbox { cm}=70\mbox { cm}$ .

Di sicuro il quadrilatero sarà circoscrivibile perchè, affinchè lo sia, deve essere uguale la somma dei lati opposti, ma ciò abbiamo appena visto che è vero per costruzione.

Per avere il raggio ci serve calcolare l’area del quadrilatero:

$A_{ABCD}=2A_{ABC}=2\frac12 (AC \cdot BC)=(15\cdot 20)\mbox { cm}^2=300\mbox { cm}^2$ .

Calcoliamo il raggio quindi:

$r=\frac {A}{p}=\frac {300}{\frac 12 70}\mbox { cm}=\frac {60}{7} \mbox { cm}$

Altri esercizi simili:

(Questa pagina è stata visualizzata da 73 persone)

Matebook

La matematica spiegata passo passo

Esercizio 24 Problemi di geometria

Lascia un commento Annulla risposta