Esercizio 14 Problemi di geometria

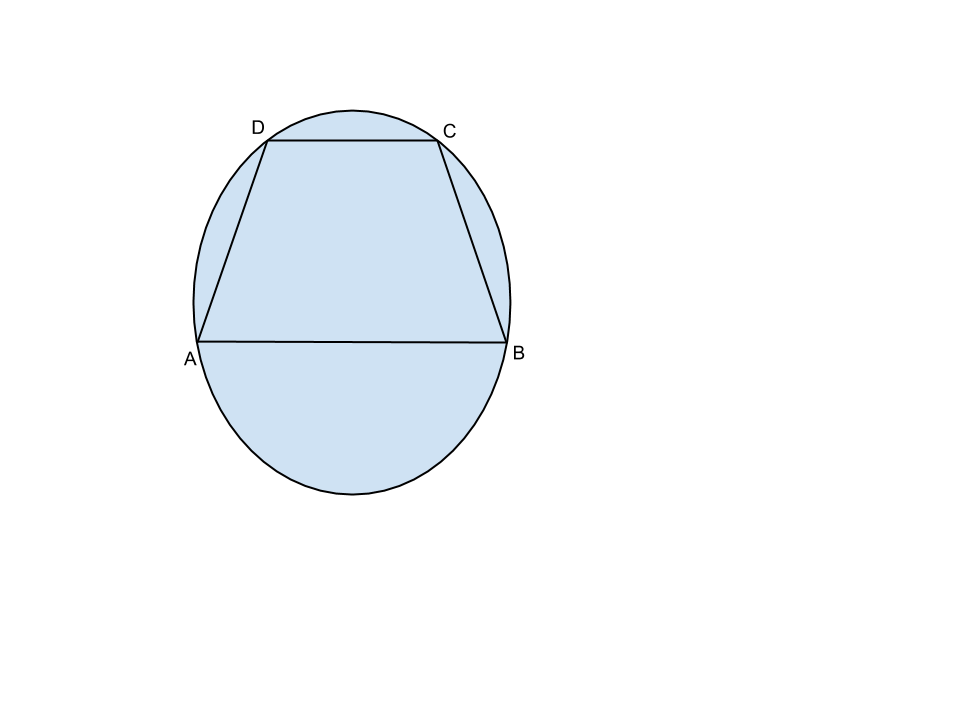
Traccia

Un trapezio $ABCD$ è circoscritto ad una circonferenza ed è $AB$ la base maggiore, $CD$ la base minore, $AD$ il lato obliquo minore. Si sa che

$\frac 25 AB + \frac 23 AD=88 \mbox{ cm } \quad CB-CD= 6 \mbox{ dm } \quad \mbox { e } \quad AD+BC=14 \mbox { dm}$

. Determinare i lati del trapezio e, successivamente, l’area. (Porre $AB=x$ e $AD=y$ ).

Svolgimento

Dai dati avremo che:

$AB+CD=AD+BC$ , per definizione di circonferenza inscritta.

Poniamo come suggerimento $AB=x$ e $AD=y$ , e otteniamo:

$\frac 25x + \frac 23 y =88$ .

Dalla prima però avremo che:

$CB-CD=AB-AD$ , quindi:

$x-y=60$ (notiamo che qui la misura era in decimetri, non in centimetri!!!)

Risolviamo quindi il sistema:

$\begin {cases} \frac 25x + \frac 23 y =88 \\ x-y=60 \end{cases}$

$\begin {cases} \frac 25(60+y) + \frac 23 y =88 \\ x=60+y \end{cases}$

$\begin {cases} 24+\frac 25y + \frac 23 y =88 \\ x=60+y \end{cases}$

$\begin {cases} \frac {6+10}{15} y =64 \\ x=60+y \end{cases}$

$\begin {cases} \frac {16}{15} y =64 \\ x=60+y \end{cases}$

$\begin {cases} y =60 \\ x=60+60=120 \end{cases}$

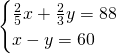
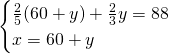
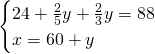
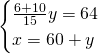
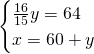
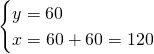
Quindi avremo:

$AB=120 \mbox{ cm }$

$AD=60 \mbox{ cm }$ .

Sapevamo anche che:

$AD+BC=140 \mbox{ cm }$ , quidni:

$BC=80 \mbox{ cm }$ e

$CD=BC-60 \mbox{ cm }=20\mbox{ cm }$ .

Per ricavare l’altezza usiamo un artificio, sapendo che per costruzione AOD e BOC sono retti.

Chiamiamo $AK=x$ e $KD=y$ , e avremo che.

$x+y=60$ , ma sfruttando le uguaglianze dei segmenti di tangenza, avremo anche che:

$BP=120-x$ e

$PC=20-y$ .

Sapendo che entrambi i triangoli considerati sono rettangoli, avremo quindi che:

$r^2=AK \cdot KD = BP\cdot PC$

Andiamo a risolvere il sistema:

$\begin{cases} x+y=60 \\ xy=(120-x)(20-y) \end{cases}$

$\begin{cases} x=60-y \\ (60-y)y=(120-(60+y))(20-y) \end{cases}$

$\begin{cases} x=60-y \\ 60y-y^2=(60+y)(20-y) \end{cases}$

$\begin{cases} x=60-y \\ 60y-y^2=1200-60y+20y-y^2 \end{cases}$

$\begin{cases} x=60-y \\ 100y=1200 \end{cases}$

$\begin{cases} x=60-12=48 \\ y=12 \end{cases}$

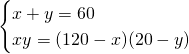
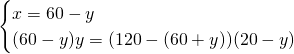
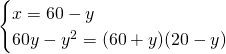
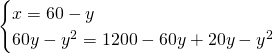
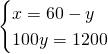
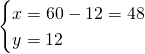
Ora possiamo ricavare il raggio:

$r= \sqrt {x \cdot y}=\sqrt {48 \cdot 12}\mbox{ cm }=24 \mbox{ cm }$

Quindi l’area sarà data dalla formula inversa del raggio:

$A=r \cdot p= 24 \cdot \frac 12 (120+80+20+60) \mbox{ cm }^2=3360\mbox{ cm }^2$

Altri esercizi simili:

(Questa pagina è stata visualizzata da 54 persone)

Lascia un commento Annulla risposta