Claudio scrive: Problema di geometria risolvibile con equazioni

Pubblicato il 14 Ottobre 2013 da Lo StaffLascia un commento

Oggetto: Problema di geometria risolvibile con equazioni

Corpo del messaggio:
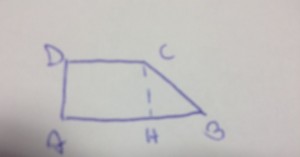
Un trapezio rettangolo con la base maggiore AB, AD il lato perpendicolare alle basi ed è H il punto d’incontro di AB con la perpendicolare alle basi condotta per l’estremo C della base minore. Determina HB, CH, BC sapendo che CH=4/3HB e che BC+CH=45cm. Poi sapendo che AB= 42cm determina perimetro e area del trapezio.
Risultato:HB=15; CH=AD=20;BC=25;114cm; 690CM2

Dai dati sappiamo che:

$CH=\frac 43 HB$

$BC+CH=45 \mbox { cm}$

Poniamo $CH=x$ , così da avere:

$HB=\frac 34 x$

$BC=45-x$

Sfruttando il teorema di Pitagora, otteniamo:

$CH^2=BC^2-BH^2$

Da cui:

$x^2=(45-x)^2-(\frac 34x)^2$

$x^2=2025-90x+x^2-\frac {9}{16}x^2$

svolgendo il minimo comune multiplo otteniamo:

$9x^2+1440x-32400=0$

$x^2+160x-3600=0$

$(x-20)(x+180)=0$

Essendo CH la misura di un lato, questa non può essere negativa e quindi:

$x=20$

$CH=20 \mbox { cm}$

$HB=15 \mbox { cm}$

$BC=25 \mbox { cm}$

Sappiamo anche che $AB=42 \mbox { cm}$ , e quindi possiamo calcolare anche CD:

$CD=AB-HB=(42-15)\mbox { cm}=27\mbox { cm}$ .

AD sarà uguale a CH per costruzione, quindi:

$2p=(42+25+27+20) \mbox { cm}=114 \mbox { cm}$ :

$A=\frac {(B+b) \cdot h}{2}=\frac {(42+27)\cdot 20}{2}\mbox { cm}^2=690 \mbox { cm}^2$

(Questa pagina è stata visualizzata da 171 persone)

Lascia un commento Annulla risposta

Devi essere connesso per inviare un commento.