Oggetto: Soluzione di un problema di terza Media sul teorema di Euclide per mio nipote

Corpo del messaggio:
In un triangolo rettangolo l’altezza relativa all’ipotenusa misura 300 cm e divide l’ipotenusa stessa in due parti la cui differenza misura 84 cm Calcolane perimetro ed area.  [2p = 720 ; A  = 21600]
Grazie

Risposta dello staff

Sapendo l’altezza e le due relative parti in cui è divisa possiamo sfruttare il teorema di Euclide per ricavare i due cateti.

Sappiamo che, chiamando x e y le due parti in cui è divisa l’ipotenusa:

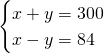
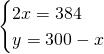
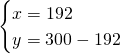
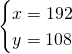
Da cui avremo:

Troviamo il perimetro:

e l’area:

 

(Questa pagina è stata visualizzata da 60 persone)