Traccia
![]()
Svolgimento
![]()
Distingueremo due casi separati e poi uniremo il tutto:
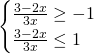
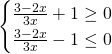
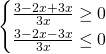
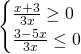
Da queste, senza eseguire troppi calcoli osserveremo che le soluzioni sono:
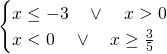
Inserendo tutto in un grafico otterremo la soluzione:
| I | +++ | +++ | +++ | |
| II | +++ | +++ | +++ | |
| Ris | +++ | +++ |
Dalla tabella si evince che il risultato sarà:
![]()
Altri esercizi simili
- Esercizio 1 Disequazioni del tipo |f(x)| >< k, con k>0
- Esercizio 2 Disequazioni del tipo |f(x)| >< k, con k>0
- Esercizio 3 Disequazioni del tipo |f(x)| >< k, con k>0
- Esercizio 4 Disequazioni del tipo |f(x)| >< k, con k>0
- Esercizio 5 Disequazioni del tipo |f(x)| >< k, con k>0
- Esercizio 6 Disequazioni del tipo |f(x)| >< k, con k>0
(Questa pagina è stata visualizzata da 121 persone)