Problemi di geometria piana
- Determinare gli angoli di un triangolo isoscele sapendo che l’angolo al vertice è doppio di ciascuno degli angoli adiacenti alla base.
- Determinare l’ampiezza degli angoli di un triangolo isoscele sapendo che ciascuno degli angoli alla base è i
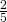 dell’angolo al vertice
dell’angolo al vertice - In un triangolo isoscele l’angolo al vertice è il quadruplo di ciascun angolo adiacente alla base. Calcolare le ampiezze degli angoli del triangolo.
- Determinare gli angoli di un triangolo sapendo che il primo è i
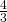 del secondo e che il terzo angolo supera di 30
del secondo e che il terzo angolo supera di 30 il secondo.
il secondo. - Determinare gli angoli di un triangolo sapendo che il primo è i
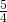 del secondo e che il terzo angolo supera di 15
del secondo e che il terzo angolo supera di 15 la metà del secondo.
la metà del secondo. - Determinare gli angoli di un triangolo sapendo che il primo è
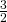 del secondo e che il terzo angolo supera di 30
del secondo e che il terzo angolo supera di 30 la somma degli altri due.
la somma degli altri due. - Determinare gli angoli di un quadrangolo sapendo che due angoli sono retti e che il terzo è i
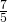 del quarto.
del quarto. - Il perimetro di un rettangolo è 120 cm; calcolare l’area del rettangolo sapendo che la base è tripla dell’altezza.
- In un rettangolo l’altezza è i
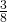 della base e la somma dei
della base e la somma dei 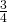 della base con i
della base con i 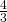 dell’altezza è 20 cm. Determinare il perimetro e l’area del rettangolo.
dell’altezza è 20 cm. Determinare il perimetro e l’area del rettangolo. - In un rettangolo i
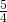 della base superano di 17 cm l’altezza; determinare perimetro e area del rettangolo sapendo che la somma dei
della base superano di 17 cm l’altezza; determinare perimetro e area del rettangolo sapendo che la somma dei 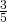 della base con i
della base con i 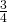 dell’altezza è 18 cm.
dell’altezza è 18 cm. - La somma delle diagonali di un rombo è 60 cm e i
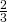 della maggiore aggiunti alla metà della minore danno 36 cm. Determinare l’area del rombo.
della maggiore aggiunti alla metà della minore danno 36 cm. Determinare l’area del rombo. - In un trapezio isoscele il rapporto delle basi è
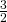 e il lato obliquo è i
e il lato obliquo è i 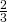 della base minore. Determinare il perimetro del trapezio sapendo che la somma tra la base maggiore e metà del lato obliquo è 66 cm.
della base minore. Determinare il perimetro del trapezio sapendo che la somma tra la base maggiore e metà del lato obliquo è 66 cm. - Determinare le diagonali di un rombo sapendo che la maggiore è
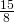 della minore e la loro differenza è 21,14 m.
della minore e la loro differenza è 21,14 m.
Altri hanno visualizzato anche
- Esercizi sulle equazioni di primo grado
- Problemi di geometria piana risolubili con equazioni di primo grado
- Problemi risolubili con equazioni numeriche intere di primo grado
- Problemi risolubili con il teorema di Pitagora
- Radici di equazioni di primo grado
(Questa pagina è stata visualizzata da 2440 persone)
Menomale che esiste qualcuno che scrive questi problemi altrimenti non saprei neanche cos’é un quadrangolo…:)