Problemi risolubili con il teorema di Pitagora

-8

Tracce:

  1. Il perimetro di un triangolo isoscele è di 64 cm e il lato supera di 5 cm i 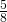\frac 5 8 della base. Determinare le lunghezze dei lati e dell’altezza relativa alla base.
  2. Nel triangolo isoscele ABC, la base BC supera di 22 cm l’altezza AH. Determinare il perimetro del triangolo sapendo che: \frac 4 5 \overline {BC} + \frac 7 4 {AH}=38 cm.
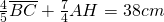  3. In un triangolo isoscele la somma del lato e dei 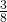\frac 38 dell’altezza relativa alla base è 26 m; si sa inoltre che l’altezza supera di 12 m la quinta parte del lato stesso. Determinare la lunghezza della base e l’area del triangolo.
  4. In un trapezio rettangolo la base maggiore è doppia della minore e supera l’altezza di 10 m. Determinare la lunghezza del perimetro e l’area del trapezio sapendo che la somma dell’altezza e dei 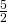\frac 5 2 della base minore è 26 m.
  5. Del rettangolo ABCD si conosce la base AB=64 cm e l’altezza BC=1 dm. Si prenda su AB un punto  M e su CD un punto N in modo che sia DN=2AM e che l’area del trapezio AMND sia 360 cm^2. Determinare il perimetro dei due trapezi AMND e MBCN.(Porre \overline {AM}=x).
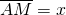  6. In un trapezio isoscele la somma delle basi è 32 cm e la maggiore è i 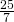\frac {25} 7 della minore; si sa che l’altezza è di 12 cm. Determinare l’area e il perimetro del trapezio.
  7. Nel trapezio isoscele ABCD la base minore AB è i 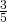\frac 3 5 della base maggiore CD e la differenza delle basi è 8 cm. Determinare l’area e il perimetro del trapezio sapendo che l’altezza è di 3 cm.
  8. In un rombo ABCD la diagonale BD è i 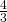\frac 4 3 della diagonale AC e si sa che 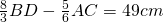\frac 8 3 BD - \frac 5 6 AC=49 cm.Trovare il perimetro del rombo.
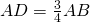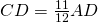  9. Nel trapezio rettangolo ABCD , AB è la base maggiore e AD il lato perpendicolare alle basi. Si sa che AD=\frac 3 4 AB e CD=\frac {11}{12}AD; la somma delle basi è 54 cm. Dopo aver determinato la base maggiore AB, determinare l’area del trapezio e il perimetro.
  10. Nel triangolo isoscele ABC, AH è l’altezza relativa alla base BC ed è 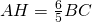AH=\frac 6 5 BC. Determinare il perimetro del triangolo sapendo che \frac 4 5 BC + \frac 5 6 AH=36 cm.

 

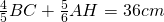Altri hanno visualizzato:

(Questa pagina è stata visualizzata da 1415 persone)

Lascia un commento