Risoluzione e spiegazione del seguente problema di geometria con due o più incognite
Determinare gli angoli di un triangolo sapendo che sottraendo dai ![]() del primo i
del primo i ![]() del secondo si ottengono
del secondo si ottengono ![]() e che aggiungendo al secondo la metà del terzo si ottengono
e che aggiungendo al secondo la metà del terzo si ottengono ![]()
Risolviamo questo sistema:
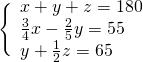
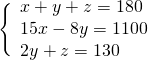
Usiamo il metodo di Cramer:
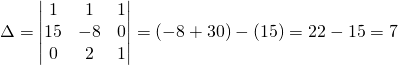
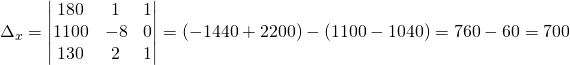
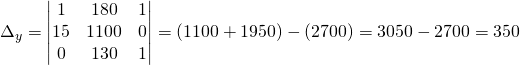
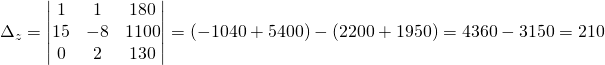
![]()
![]()
![]()
Altri esercizi simili:
(Questa pagina è stata visualizzata da 275 persone)