Risoluzione e spiegazione del seguente problema di geometria con due o più incognite
- Determinare gli angoli di un triangolo sapendo che la somma di due di essi supera di
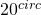 il terzo angolo e che la somma della sesta parte del primo con la quarta parte del secondo uguaglia la quarta parte del terzo.
il terzo angolo e che la somma della sesta parte del primo con la quarta parte del secondo uguaglia la quarta parte del terzo.
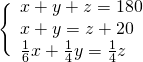
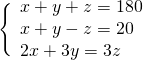
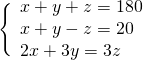
Sottraendo la seconda dalla prima otteniamo subito un’equazione nella sola incognita ![]() :
:
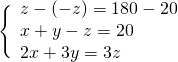
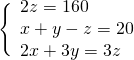
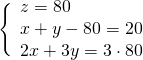
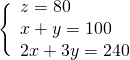
Troviamo la ![]() nella seconda equazione.
nella seconda equazione.
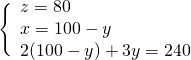
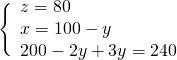
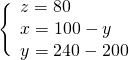
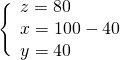
Altri esercizi simili:
- Problema 1 di geometria con due o più incognite
- Problema 2 di geometria con due o più incognite
- Problema 3 di geometria con due o più incognite
- Problema 4 di geometria con due o più incognite
- Problema 5 di geometria con due o più incognite
(Questa pagina è stata visualizzata da 224 persone)