Si definisce isometria piana ogni trasformazione geometrica piana che a due punti qualsiasi ![]() e
e ![]() del piano fa corrispondere rispettivamente i punti
del piano fa corrispondere rispettivamente i punti ![]() e
e ![]() , in modo che risulti
, in modo che risulti ![]() .
.
Ogni isometria piana trasforma una figura piana in una figura a essa congruente e conserva l’allineamento, il parallelismo, l’incidenza e la perpendicolarità. Le isometrie piane si suddividono in isometrie dirette e isometrie invertenti. Tra le isometrie piane si distinguono: le simmetrie centrali, le simmetrie assiali, le traslazioni e le rotazioni.
- Simmetria centrale rispetto a un generico punto
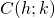
Poichè ![]() è punto medio del segmento
è punto medio del segmento ![]() , si ha:
, si ha:
- Isometria diretta
- il centro di simmetria
 è l’unico punto unito;
è l’unico punto unito; - le rette del fascio proprio con sostegno nel punto
 sono le uniche rette unite, ma non fisse.
sono le uniche rette unite, ma non fisse.
- Simmetria centrale rispetto all’origine
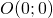
![]()
- Caso particolare del precedente con
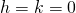 .
.
- Simmetria assiale ortogonale rispetto all’asse

![]()
- Isometria invertente;
- i punti dell’asse
 sono gli unici punti uniti;
sono gli unici punti uniti; - l’asse
 è l’unica retta fissa;
è l’unica retta fissa; - le rette perpendicolari all’asse
 sono rette unite ma non fisse.
sono rette unite ma non fisse.
- Simmetria assiale ortogonale rispetto all’asse
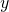
![]()
- Isometria invertente;
- i punti dell’asse
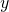 sono gli unici punti uniti;
sono gli unici punti uniti; - l’asse
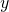 è l’unica retta fissa;
è l’unica retta fissa; - le rette perpendicolari all’asse
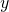 sono rette unite ma non fisse.
sono rette unite ma non fisse.
- Simmetria assiale ortogonale
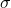 rispetto alla bisettrice di equazione
rispetto alla bisettrice di equazione 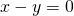
![]()
- Isometria invertente;
- i punti della bisettrice sono gli unici punti uniti;
- la bisettrice è l’unica retta fissa;
- le rette perpendicolari alla bisettrice sono rette unite ma non fisse.
- Simmetria assiale ortogonale
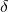 rispetto alla bisettrice di equazione
rispetto alla bisettrice di equazione 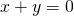
![]()
- Isometria invertente;
- i punti della bisettrice sono gli unici punti uniti;
- la bisettrice è l’unica retta fissa;
- le rette perpendicolari alla bisettrice sono rette unite ma non fisse.
- Simmetria assiale ortogonale rispetto a una generica retta di equazione
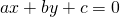
![]() e
e ![]() sono simmetrici rispetto alla retta
sono simmetrici rispetto alla retta ![]() è l’asse del segmento
è l’asse del segmento ![]()
![]() ,
, ![]() ,
, ![]() ,
,
quindi le equazioni della simmetria rispetto a ![]() si ricavano risolvendo in
si ricavano risolvendo in ![]() e
e ![]() il sistema:
il sistema:
![]()
- Isometria invertente;
- i punti della retta
 asse di simmetria sono gli unici punti uniti;
asse di simmetria sono gli unici punti uniti; - la retta
 è l’unica retta fissa;
è l’unica retta fissa; - le rette perpendicolari alla retta
 sono rette unite ma non fisse.
sono rette unite ma non fisse.
- Traslazione
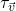 di vettore
di vettore 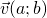
![]()
- Isometria diretta;
- non ci sono punti uniti;
- le rette parallele alla retta su cui giace il vettore
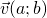 sono le uniche rette unite ma non fisse.
sono le uniche rette unite ma non fisse.
- Rotazione
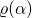 di centro
di centro 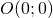 e angolo orientato
e angolo orientato 
![]()
- Isometria diretta;
- il centro di rotazione
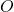 è l’unico punto unito;
è l’unico punto unito; - se
 la rotazione coincide con la simmetria centrale di centro
la rotazione coincide con la simmetria centrale di centro 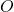 ; le rette le fascio proprio con sostegno nel punto
; le rette le fascio proprio con sostegno nel punto 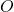 sono rette unite ma non fisse.
sono rette unite ma non fisse.
Altri hanno visualizzato anche:
- Affinità
- Dilatazioni
- Isometrie
- Omotetie
- Similitudini
- Trasformazioni relative al sistema di riferimento
(Questa pagina è stata visualizzata da 453 persone)