Oggetto: esercizio sulla parabola e tangenza
Corpo del messaggio:
Qual ´e l’equazione della parabola con asse di simmetria paral-
lelo all’asse delle ordinate passante per il punto A (0, 1) e
tangente alla retta di equazione y = x in P (1, 1)?
grazie in anticipo
Risposta dello staff
Avendo l’asse parallelo all’asse delle ordinate, allora l’equazione sarà del tipo:
![]()
Passando per A e per P otteniamo:
![]()
![]()
![]()
![]()
Di conseguenza l’equazione sarà del tipo:
![]()
Imponiamo che sia tangente alla retta ![]() nel punto P:
nel punto P:

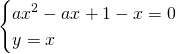
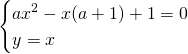
Ricaviamo il ![]() nella prima equazione:
nella prima equazione:
![]()
Imponendo che il ![]() sia uguale a 0, otteniamo che
sia uguale a 0, otteniamo che ![]() e di conseguenza l’equazione della parabola sarà:
e di conseguenza l’equazione della parabola sarà:
![]()
(Questa pagina è stata visualizzata da 40 persone)