Traccia
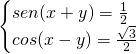
Svolgimento
Per risolvere questo sistema semplicemente eguagliare l’argomento degli angoli che fanno si che il ![]() sia uguale a
sia uguale a ![]() e il
e il ![]() sia uguale a
sia uguale a ![]() :
:
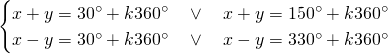
In questo caso svolgiamo quattro sistemi differenti:
Da cui, sommando le due e scrivendo il risultato nella prima equazione e sottraendole due e scrivendo il risultato nella seconda otteniamo:
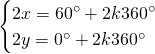
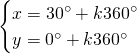
Da cui, sommando le due e scrivendo il risultato nella prima equazione e sottraendole due e scrivendo il risultato nella seconda otteniamo:
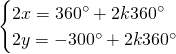
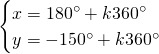
Da cui, sommando le due e scrivendo il risultato nella prima equazione e sottraendole due e scrivendo il risultato nella seconda otteniamo:
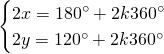
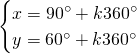
Da cui, sommando le due e scrivendo il risultato nella prima equazione e sottraendole due e scrivendo il risultato nella seconda otteniamo:
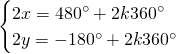
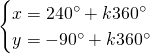
Altri esercizi simili
(Questa pagina è stata visualizzata da 1004 persone)
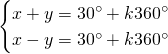
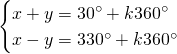
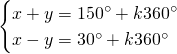
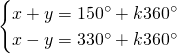
Cito quanto sopra scritto: “Per risolvere questo sistema semplicemente eguagliare l’argomento degli angoli che fanno si che il sen sia uguale a 1 e il cos sia uguale a \frac {\sqrt 3}2:”
Beh…cari signori… a casa mia l’equazione relativa al SEN(X+Y)=1 la scriverei:
x+y= 90°+k360° (perchè sen90°=1 con periodicità di 360°) e non x+y=30°+k360°!!!
Il resto non oso neanche guardarlo.
Correggete, prego.
Dispiace sempre leggere certi commenti. Dispiace vedere come l’aiuto di qualcuno lo si debba ogni volta cercare di denigrare. Dispiace vedere come qualcuno che si suppone conosca la matematica non noti che questo sia solo un errore di battitura in quanto il resto dell’esercizio è stato svolto come se sen(x+y) fosse uguale ad 1/2.
Ringraziamo comunque per l’aver fatto notare l’errore, che è stato corretto, ma sarebbe gradito un tono più consono.