Traccia
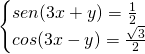
Svolgimento
Per risolvere questo sistema semplicemente eguagliare l’argomento degli angoli che fanno si che il ![]() sia uguale a
sia uguale a ![]() e il
e il ![]() sia uguale a
sia uguale a ![]() :
:
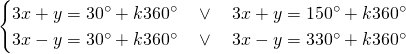
In questo caso svolgiamo quattro sistemi differenti:
Da cui, sommando le due e scrivendo il risultato nella prima equazione e sottraendole due e scrivendo il risultato nella seconda otteniamo:
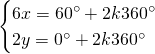
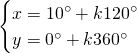
Da cui, sommando le due e scrivendo il risultato nella prima equazione e sottraendole due e scrivendo il risultato nella seconda otteniamo:
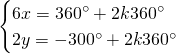
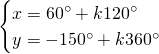
Da cui, sommando le due e scrivendo il risultato nella prima equazione e sottraendole due e scrivendo il risultato nella seconda otteniamo:
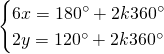
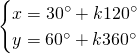
Da cui, sommando le due e scrivendo il risultato nella prima equazione e sottraendole due e scrivendo il risultato nella seconda otteniamo:
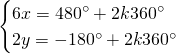
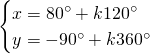
Altri esercizi simili
(Questa pagina è stata visualizzata da 609 persone)
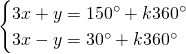
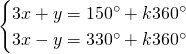
c’è qualcosa di sbagliato nella traccio o nell’individuare l’angolo per cui il seno è uguale a 1? può essere anche una mia svista.
C’è un errore nella traccia… ovviamente dal seguente svolgimento si capiva non fosse 1!! 🙂
Grazie 1000 per avercelo fatto notare!!! Riveduto e corretto