Traccia
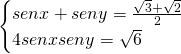
Svolgimento
Se riscriviamo il sistema in questo modo:
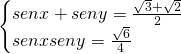
ci ritroviamo nella situazione di un sistema a noi già noto, dove abbiamo la somma e il doppio prodotto delle due radici, ovvero, rivedendolo in questo modo (usiamo ![]() come incognita per evitare ridondanze):
come incognita per evitare ridondanze):
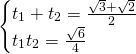
e risolveremmo l’equazione di secondo grado:
![]() .
.
Ma senza fare grossi calcoli ci accorgiamo subito che le due soluzioni sono implicite nell’esercizio, infatti le coppie di risultati sono:
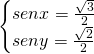 oppure
oppure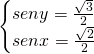
Troviamo solo una soluzione, tanto l’altra sarà speculare, e basterà scambiare ![]() con
con ![]() . Analizziamo la prima, e avremo:
. Analizziamo la prima, e avremo:
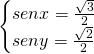

Altri esercizi simili
- Esercizio 1 Sistemi di equazioni goniometriche
- Esercizio 2 Sistemi di equazioni goniometriche
- Esercizio 3 Sistemi di equazioni goniometriche
- Esercizio 4 Sistemi di equazioni goniometriche
- Esercizio 5 Sistemi di equazioni goniometriche
(Questa pagina è stata visualizzata da 547 persone)