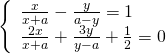
alla 5 poni ![]() e
e ![]() da cui:
da cui:
![]()
![]()
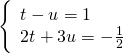
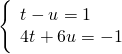
Usando il metodo di sostituzione troviamo la ![]() nella prima.
nella prima.
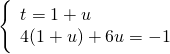
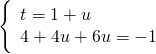
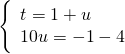
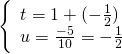
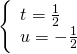 .
.
Quindi:
![]()
![]()
Altri hanno visualizzato:
- Sistemi che si risolvono con artifici 1
- Sistemi che si risolvono con artifici 2
- Sistemi che si risolvono con artifici 3
- Sistemi che si risolvono con artifici 4
- Sistemi che si risolvono con artifici 5
(Questa pagina è stata visualizzata da 334 persone)