Quando parliamo di integrale definito, senza soffermarci troppo su elementi troppo teorici, parliamo di quella funzione che assume l’importante significato geometrico di area con segno; quindi, esiste una relazione fondamentale tra l’integrale definito di una funzione ![]() in un intervallo
in un intervallo ![]() , e l’area
, e l’area ![]() della regione piana delimitata dal grafico della funzione e dall’asse delle ascisse.
della regione piana delimitata dal grafico della funzione e dall’asse delle ascisse.
Precisamente diremo che:
- se
![Rendered by QuickLaTeX.com f(x)\ge 0 \forall x \in [a;b] \rightarrow A=\int^b_a f(x) \mathrm {d}x](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-8192419d25c6a5ada20d468763ace2ec_l3.png) ;
; - se
![Rendered by QuickLaTeX.com f(x)\le 0 \forall x \in [a;b] \rightarrow A= -\int^b_a f(x) \mathrm {d}x](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-913c338f1495667e516de629105ad26f_l3.png) .
.
Posto per definizione che:
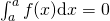 ,
,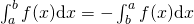 ,
,
l’integrale definito soddisfa importanti proprietà:
- l’integrale definito è un’operatore lineare:
![Rendered by QuickLaTeX.com \int_a^b [h_1f_1(x) + h_2f_2(x)+...+ h_nf_n(x)] \mathrm{d}x=h_1 \int_a^b f_1(x) \mathrm{d}x + h_2 \int_a^b f_2(x) \mathrm{d}x + ... + h_n \int_a^b f_n(x) \mathrm{d}x](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-5f7bee70c608b827403cdff4370b2e52_l3.png) ,
,
- Additività dell’integrale definito rispetto all’intervallo di integrazione. Se
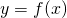 è una funzione continua nell’intervallo
è una funzione continua nell’intervallo ![Rendered by QuickLaTeX.com [a;b]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-22695be398ca102e6215f2e853eaf81f_l3.png) risulta:
risulta:
![]() .
.
- Confronto tra gli integrali definiti di due funzioni.
Se ![]() e
e ![]() sono due funzioni continue, tali che
sono due funzioni continue, tali che ![]() , risulta:
, risulta:
![]() .
.
- Integrale del valore assoluto di una funzione.
Se ![]() è una funzione continua nell’intervallo
è una funzione continua nell’intervallo ![]() risulta:
risulta:
![]() .
.
Altri hanno visualizzato anche
- Esercizi Integrali
- Esercizi sugli integrali immediati
- Integrali definiti
- Integrali per sostituzione
- Integrazione di funzioni razionali fratte
- Integrazione per parti
(Questa pagina è stata visualizzata da 1262 persone)