Esercizio 3 integrali per parti

$\int e^x sin x \mathrm{d}x$

Per questa funzione è indifferente la scelta, perchè sono funzioni “circolari”, e quindi bisognerà applicare due volte il processo per parti.

$f(x)=senx \rightarrow f'(x)= cosx$

$g'(x)= e^x \rightarrow g(x)= e^x$

$\int e^x sin x \mathrm{d}x = e^xsinx-\int e^x cos x \mathrm{d}x$

$f(x)=-cosx \rightarrow f'(x)= sinx$

$g'(x)= e^x \rightarrow g(x)= e^x$

$\int e^x sin x \mathrm{d}x = e^xsinx+\int e^x (-cos x) \mathrm{d}x =e^xsinx -e^xcosx-\int e^x sin x \mathrm{d}x \rightarrow \int e^x sin x \mathrm{d}x = e^xsinx -e^xcosx-\int e^x sin x \mathrm{d}x \rightarrow 2\int e^x sin x \mathrm{d}x= e^x(cosx-sinx) \rightarrow \int e^x sin x \mathrm{d}x= \frac {e^x(cosx-sinx)}{2}+c$

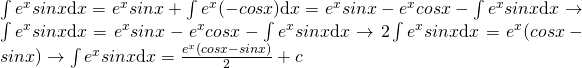
Altri hanno visualizzato anche:

Esercizio 1 integrali per parti
Esercizio 2 integrali per parti
Esercizio 3 integrali per parti
Esercizio 4 integrali per parti
Esercizio 5 integrali per parti

(Questa pagina è stata visualizzata da 224 persone)

Matebook

La matematica spiegata passo passo

Esercizio 3 integrali per parti

Lascia un commento Annulla risposta