![]()
Essendoci un polinomio di secondo grado e la funzione ![]() , anche in questo caso dovremo utilizzare due volte l’integrazione per parti in modo da abbassare il grado del polinomio all’interno dell’integrale.
, anche in questo caso dovremo utilizzare due volte l’integrazione per parti in modo da abbassare il grado del polinomio all’interno dell’integrale.
![]()
![]()
![]()
![]()
![]()
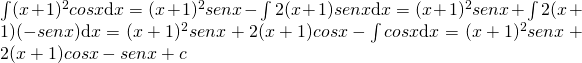
Altri hanno visualizzato anche:
- Esercizio 1 integrali per parti
- Esercizio 2 integrali per parti
- Esercizio 3 integrali per parti
- Esercizio 4 integrali per parti
- Esercizio 5 integrali per parti
(Questa pagina è stata visualizzata da 202 persone)
La soluzione dell’esercizio 5 mi sembra che manchi del fattore 2 davanti a senx. Vorrei una conferma. Grazie.
Saluti.