L’iperbole è il luogo geometrico dei punti ![]() del piano per i quali il valore assoluto della differenza delle loro distanze da due punti fissi
del piano per i quali il valore assoluto della differenza delle loro distanze da due punti fissi ![]() ,
, ![]() , detti fuochi, si mantiene costante (tale valore rappresenta la lunghezza dell’asse trasverso).
, detti fuochi, si mantiene costante (tale valore rappresenta la lunghezza dell’asse trasverso).
Per l’iperbole con centro nell’origine ![]() e assi di simmetria coincidenti con gli assi cartesiani si distinguono due casi:
e assi di simmetria coincidenti con gli assi cartesiani si distinguono due casi:
| asse trasverso asse |
asse trasverso asse |
|
| equazione canonica | ||
| coordinate vertici | ||
| coordinate vertici non reali | ||
| coordinate fuochi | ||
| relazione tra i parametri | |
|
| lunghezza asse trasverso | |
|
| lunghezza asse non trasverso | |
|
| distanza focale | |
|
| eccentricità |
|
|
| equazione asintoti |
L’iperbole è detta traslata se ha centro in un punto ![]() e assi di simmetria paralleli agli assi cartesiani, di equazioni
e assi di simmetria paralleli agli assi cartesiani, di equazioni ![]() e
e ![]() . Si presentano due casi:
. Si presentano due casi:
| asse trasverso parallelo all’asse |
asse trasverso parallelo all’asse |
|
| equazione canonica | ||
| coordinate vertici | ||
| coordinate vertici non reali | ||
| coordinate fuochi | ||
| relazione tra i parametri | |
|
| lunghezza asse trasverso | |
|
| lunghezza asse non trasverso | |
|
| distanza focale | |
|
| eccentricità |
|
|
| equazione asintoti |
L’iperbole riferita agli assi aventa asse trasverso di lunghezza uguale a quella dell’asse non trasverso, ovvero ![]() , viene detta iperbole equilatera riferita agli assi, e ha equazione:
, viene detta iperbole equilatera riferita agli assi, e ha equazione:
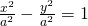 , ovvero
, ovvero 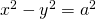 , se i fuochi appartengono all’asse
, se i fuochi appartengono all’asse  ,
,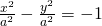 , ovvero
, ovvero 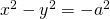 , se i fuochi appartengono all’asse
, se i fuochi appartengono all’asse 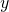 .
.
In entrambi i casi la relazione ![]() diventa
diventa ![]() , da cui
, da cui ![]() . Perciò l’eccentricità risulta essere
. Perciò l’eccentricità risulta essere
![]()
e gli asintoti coincidono con le bisettrici dei quadranti, di equazioni ![]() .
.
Se si applica una rotazione di 45°, o di 135°, si ottiene l’iperbole equilatera riferita agli asintoti, con equazione ![]() ,
, ![]() .
.
Si distinguono due casi, dipendenti dal segno della costante ![]() .
.
Vertici: ![]() e
e ![]() ;
;
![]() ,
, ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;![]() .
.
Vertici: ![]() e
e ![]() ;
;
![]() ,
, ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;![]() .
.
Se si applica una traslazione all’iperbole equilatera riferita agli asintoti si ottiene la funzione omografica di equazione
![]() ,
, ![]() , con
, con ![]() e
e ![]() ,
,
avente dominio ![]() .
.
Il centro di simmetria ha coordinate
![]() ,
,
le equazioni degli asintoti sono
![]() e
e ![]() ;
;
gli assi di simmetria sono paralleli alle bisettrici dei quadranti, passano per il centro ![]() e hanno equazioni
e hanno equazioni
![]() .
.
Si osserva che se ![]() , la funzione omografica degenera nella retta di equazione
, la funzione omografica degenera nella retta di equazione
![]() ,
,
mentre se ![]() , ovvero
, ovvero ![]() ,
, ![]() la funzione omografica degenera nella retta di equazione
la funzione omografica degenera nella retta di equazione
![]() .
.
Altri hanno visualizzato anche
- Circonferenza
- Ellisse
- Iperbole
- Parabola
- Punto retta
- Retta
- Rette tangenti ad una conica
- Trasformazioni geometriche piane
- Triangoli
(Questa pagina è stata visualizzata da 411 persone)